Princípios Básicos da Análise de Distribuição de Tamanho de Partícula – Parte 2

Download



Distribuição por Número e por Volume 

 

  O exemplo acima é do New Scientist (31 de outubro de 1991). No espaço, orbitando a Terra, existe um número significativo de partículas cuja órbita foi intencionalmente colocada lá pelo homem. Cientistas também classificaram estas partículas com base em seu tamanho. Se examinarmos o terceiro parágrafo acima, podemos deduzir que exatamente 99,3% de todas as partículas são incrivelmente pequenas. Essa avaliação é baseada em números. No entanto, se examinarmos o quarto parágrafo, podemos deduzir que praticamente todos os objetos são precisamente entre 10-1000cm. Isto reflete a massa de cada objeto. Os números e as distribuições de massa podem ser muito diferentes, afetando suas conclusões dependendo de qual distribuição utilizar. Note que nenhuma delas é completamente precisa. Os dados são apenas analisados de forma diferente. Por exemplo, se estivermos criando um traje espacial, pode parecer fácil evitar os grandes objetos, mas também precisamos proteger contra as pequenas partículas que representam 99,3% do padrão numérico. Se calculássemos a média das distribuições na tabela acima, notaríamos que a média numérica é de cerca de 1,6cm, enquanto a média de massa é de cerca de 500cm – uma diferença bastante notável.

Conversão cruzada de distribuição por Número, Comprimento, Volume e Massa

  Medindo partículas com um microscópio eletrônico, você notará que estamos calculando o D[1,0] ou o diâmetro médio por número-comprimento. Se realmente necessitamos da média por massa ou volume, devemos converter a média numérica para a média de massa. Isso é matematicamente possível, mas devemos medir precisamente o efeito dessa conversão.

  Suponha que a tecnologia de medida elétrica tenha uma precisão de +-3%. Ao mudar de uma média numérica para uma média de massa, a precisão se torna o cubo do valor final, resultando em +-27%.

 











  Contudo, se estamos calculando a distribuição de massa ou volume com difusão a laser, a situação muda.

  Em condições de dispersão por solução, para uma amostra estável, podemos alcançar uma média de volume reciclável com erro de +-0,5%.

  Se transformarmos essa média de volume em uma média numérica, o erro ou média numérica será a raiz cúbica de 0,5%, menor que 1,0%.

  Realmente, utilizando um microscópio eletrônico para distribuições de volume ou massa, perder uma partícula de 10μ equivale a perder mil partículas de 1μ. Portanto, devemos ter em mente o grande risco das conversões cruzadas.

  Nos Sizers da Malvern, tanto o software DOS quanto o Windows calcularão diferentes diâmetros. Contudo, devemos ter cuidado ao calcular esses diâmetros. Diferentes métodos (significando) podem ser convertidos uns nos outros através das equações de transformação Hatch-Choate. Uma nota: o gráfico de típica distribuição log-normal.

 

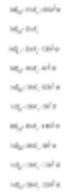
Medições e Diâmetros Derivados

  Já observamos que, ao usar a tecnologia de difração a laser da Malvern, uma distribuição de volume para analisar a energia luminosa é gerada (note que assume-se a distribuição de área inspecionada pela análise de Fraunhofer). Esta distribuição de volume pode ser convertida em qualquer número ou diâmetro linear, como mostrado acima.

  Em qualquer método analítico, devemos saber quais resultados foram convertidos (discutidos em outra seção), ou seja, saber quais diâmetros foram realmente medidos pela máquina e quais foram determinados a partir dos cálculos ou medidos diretamente.

  Algumas técnicas também podem derivar outros diâmetros de diâmetros previamente medidos. Por exemplo, um microscópio calcula D[1,0] e a partir disso, outros diâmetros podem ser obtidos.

  Uma média numérica é mais confiável do que uma média calculada. Dependendo de características derivadas (calculadas), pode-se tornar uma prática arriscada. Por exemplo, a tabela de análise de Malvern oferece uma área de superfície específica (m/cc ou m/gm).

  Não se deve confiar completamente na tabela. – Se realmente queremos uma medida específica da área de superfície, devemos usar técnicas específicas como B.E.T. ou porosimetria de mercúrio capazes de medir diretamente a área de superfície específica.

Qual número utilizar?

  Outro método que já conhecemos: medir outras propriedades (ou tamanhos) das partículas. Precisamos usar os dados para obter outras médias (D[4,3], D[3,2], etc.) de diferentes maneiras. Por que usar o número?

  Um exemplo simples de diâmetros de esferas 1 e 10 unidades. Estamos fabricando ouro, digamos. Se calcularmos a média simples dos diâmetros, temos:

 

 

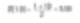
  Assim, presumimos que o tamanho médio das partículas no sistema é 5,50 unidades. Contudo, devem lembrar que estamos fabricando ouro, então o peso da substância é algo em que precisamos estar interessados.

  Por exemplo, sabendo a tendência do processo, não estaríamos interessados no fato de que existam 3,5 milhões de partículas. Em vez disso, estaríamos interessados em saber se existem 1kg ou 2kg de ouro. Sabendo que a média de massa é uma função cúbica do diâmetro significa que sabemos que a esfera de 1 unidade tem massa de 1 unidade, enquanto a esfera de 10 unidades tem massa de 1000 unidades.

  Portanto, a esfera maior compõe 1000/1001 do total de massa do sistema. Ao fazer ouro, poderíamos descartar a esfera de 1 unidade, pois perderemos menos de 0,1% do total de massa do sistema. Assim, a média numérica pode trazer conclusões incorretas sobre a massa no sistema. Isso faz D[4.3] muito mais útil.

  Neste exemplo de duas esferas, a média de momento de massa ou volume seria calculada da maneira mostrada abaixo:

 

 

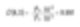
  Este número mostra onde a massa do sistema está localizada e se torna um número valioso para engenheiros de processos químicos.

  No entanto, vamos supor que estamos fabricando pastilhas de silício ou arsenieto de gálio em uma sala limpa. Aqui, se uma partícula pousar em uma pastilha, isso pode causar defeitos. Neste exemplo, o número ou concentração de partículas torna-se muito importante. Já que uma partícula é equivalente a um defeito, desejamos usar técnicas que meçam diretamente o número de partículas. Essencialmente, isso não faz diferença significante na contribuição do tamanho das partículas ou sua concentração. O número total envolve contar e registrar cada partícula. A escala de tamanho é menos crítica e só precisamos de medições até um certo nível, conforme Seção 8. Em termos de tamanho, saber a escala precisa de partículas em termos de suas contribuições de tamanho é menos relevante, e precisamos de bandas de tamanho mais abrangentes.

Média, Mediana e Moda – Estatísticas Básicas

 

Média

  Uma média aritmética qualquer dos dados. Muitas médias podem ser calculadas para partículas (veja seção D[4,3], entre outras).

Mediana

  É o valor do tamanho da partícula que divide a população em duas partes iguais. Por exemplo, 50% das amostras estão acima deste valor e 50% abaixo.

Moda

  O valor mais comum em uma distribuição de frequência, como o pico de um gráfico de frequência. Considere que esta distribuição seja normal ou gaussiana. A média, a mediana e a moda coincidem exatamente (veja Figura 4). Entretanto, considere se a distribuição for bimodal, com dois picos (veja Figura 5).

 

  As partículas de tamanho médio estarão no gráfico entre as duas distribuições. Note que não há partículas diretamente associadas a este tamanho médio. O valor mediano estará próximo da distribuição mais alta por cerca de 1%, porque esta é a divisão exata em duas distribuições. A moda será o valor do diâmetro no pico da distribuição maior, pois este é o valor mais frequente.

  Não há razão para que a média, a mediana e a moda, sujeitas à assimetria dessa distribuição, sejam ideais ou mesmo iguais, como este exemplo ilustra.

Este artigo pode ter sido traduzido automaticamente