Princípios Básicos da Análise de Granulometria-1

Baixar



Princípios Básicos da Análise de Granulometria 

O que é a Partícula?

  Perguntar isso é uma questão muito tola. No entanto, isso é fundamental em várias técnicas de análise de tamanho de partículas. O processo de dispersão e a forma do material tornam-se mais complexos na análise do tamanho de partículas.

A questão do Tamanho das Partículas

  Suponhamos que você tenha recebido uma caixa de fósforos e alguém lhe pergunte qual é o tamanho dela. Provavelmente você responderia que ela mede 20*10*5 mm. Não seria possível responder “A caixa de fósforos tem 20 mm” com precisão, pois isso seria apenas um ponto de vista sobre a dimensão. Portanto, não se pode descrever uma caixa de fósforos tridimensional apenas com uma dimensão específica. Claramente, em formas complexas como partículas de areia ou pigmentos em uma lata de tinta, a questão se torna mais complicada. Se eu fosse um gerente de controle de qualidade, gostaria que houvesse apenas um número para descrever as partículas, por exemplo, saber se o tamanho médio do último lote produzido aumentou ou diminuiu. Essa é a questão fundamental na análise de tamanho de partículas – como podemos descrever um objeto tridimensional com apenas um número?

Esferas Equivalentes

  Existe uma esfera única que pode ser representada por um único número. Se falarmos de uma esfera de 50 μm, podemos representá-la precisamente. No entanto, ao referir-se a um cubo de 50 μm, não é possível descrever suas arestas e diagonais. Caixas de fósforos com diversas características podem ser descritas por um único número, como a massa relacionada ao volume e superfície. Se houver uma técnica para medir a massa de uma caixa de fósforos, podemos convertê-la ao peso de uma esfera.

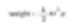
  É importante lembrar que calculamos um valor específico (2r) para o diâmetro de uma esfera que tem o mesmo peso que uma caixa de fósforos. Este é o conceito de esfera equivalente. Assumimos que uma partícula medida tem as propriedades de uma esfera, obtendo assim um valor específico (diâmetro da esfera) para representá-la.

  Isso indica que, na representação de uma partícula tridimensional, mesmo que seja menos prático para fins de controle, não precisamos usar três ou mais números.

  Podemos observar efeitos interessantes que dependem da forma do objeto, representada por um cilindro semelhante a uma esfera.

  Se a forma ou o tamanho de um cilindro mudar, o volume/peso também mudará. Entretanto, no modelo de esfera equivalente, podemos pelo menos dizer se está maior ou menor.

Diâmetro Equivalente da Esfera de um Cilindro de 100 x 20μm

  Suponha que o diâmetro de um cilindro seja D1=20μm e sua altura 100μm. Existe uma esfera com diâmetro D2, igual ao volume do cilindro. Podemos calcular o diâmetro da seguinte forma:

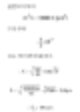
  O diâmetro esférico de um cilindro com altura de 100μm e diâmetro de 20μm é aproximadamente 40μm. A tabela abaixo mostra o diâmetro esférico de cilindros em várias proporções. A última linha pode representar partículas de argila grandes e típicas. Como possuem apenas 0,2μm de espessura em uma altura de 20μm, geralmente não se considera essa dimensão. Em relação a uma técnica que mede o volume das partículas, podemos obter um resultado em torno de 5μm. Portanto, pode ser necessário usar outras técnicas para contestar este resultado.

  Todas essas partículas cilíndricas também podem aparecer como tendo o mesmo tamanho de um filtro de 25μm, onde pode-se dizer que “todo o material é menor que 25μm”. Estas partículas têm diferentes valores quando observadas por dispersão a laser.

Diferentes técnicas de medição

  Se olharmos para uma partícula através de um microscópio, veremos uma projeção bidimensional e haverá diversos diâmetros de partícula que podem ser medidos para caracterizá-la. Ao adotar o comprimento máximo da partícula e usá-lo como o nosso tamanho, podemos dizer que é uma partícula esférica. Similarmente, se usarmos a largura mínima ou o diâmetro de Feter, isso também nos dará outra resposta sobre o tamanho da partícula. Por isso, devemos saber que cada técnica pode medir diferentes propriedades da partícula (comprimento máximo, comprimento mínimo, volume, área de superfície etc.) e, assim, ao medir de forma seletiva, podemos ter resultados diferentes daqueles mostrados por outras técnicas.

  A Figura 3 ilustra as diferentes soluções possíveis para descrever um grão de areia. Nenhuma das técnicas está errada – todas estão certas e medem diferentes propriedades da partícula. É como medir uma caixa de fósforos em cm ou polegadas (voce mede o comprimento e eu meço a largura!).

  Assim, somos forçados a medir e comparar apenas na forma de pó pela mesma técnica. Isso implica que não há um tamanho padrão para partículas como grãos de areia. Padrões devem ser esféricos por meio de comparações técnicas diferentes. No entanto, teremos um tamanho de partícula padrão para cada técnica e isso resultará na comparação dos equipamentos que usam as técnicas.

D[4,3]etc

  Pense em três esferas com tamanhos de 1, 2 e 3 unidades. Qual seria o tamanho médio entre as três partículas? No início, talvez digamos que seja 2. Como chegamos a essa resposta? Somaremos todos os valores e dividiremos pelo número total de partículas.

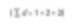
 Esse é o valor médio baseado em contagem (ou seja, o comprimento médio em termos de contagem). O número de partículas pode ser expresso na equação.

  Em termos matemáticos, é chamado de D[1,0]. Isso ocorre porque no numerador da equação acima há uma quantidade do termo diâmetro (d1) e o denominador da diâmetro (d0) não está presente. Se eu fosse um engenheiro químico, gostaria de comparar essas esferas com base na área de superfície, já que uma maior superfície oferece maior reatividade catalítica. O cálculo da área de superfície da esfera é 4πr². Portanto, ao comparar baseada na área de superfície, devemos dividir pelo número de partículas o quadrado dos diâmetros e extrair a raiz quadrada para retornar ao diâmetro médio.

  Isso novamente é a média baseada na contagem (média da contagem de superfície). Porque o número de partículas aparece na parte inferior da equação. Nós somamos todos os quadrados dos diâmetros. Assim, em termos matemáticos, é chamado de D[2,0] – a parte superior da equação foi quadrada e a parte inferior contém o termo diâmetro. Se eu fosse um major em química, gostaria de comparar a massa básica das esferas. A fórmula para o peso de uma esfera é a seguinte:

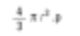
  Além disso, encontramos o valor ao dividir pela contagem de partículas e, para voltar ao diâmetro médio, extraímos a raiz cúbica.

  Isso novamente é a média baseada na contagem (média de contagem de volume ou peso). Porque o número de partículas aparece na parte inferior da equação. Em termos matemáticos, isso pode ser expresso como D[3,0].

  Os problemas das médias simples D[1,0], D[2,0] e D[3,0] estão na contagem de partículas, que é um obstáculo à aplicabilidade das fórmulas. Isso requer que muitas partículas sejam contadas e só é viável em aplicações de baixa contagem como poluição em partes por milhão ou partes por bilhão. Se todas as partículas de sílica de 1g (densidade de 2,5) fossem do tamanho de 1μm, isso representa uma simples contagem de aproximadamente 760*10^9 partículas.

Por isso, a noção de média em termos momentâneos deve ser suplementada, o que pode causar confusão. Duas médias importantes são as seguintes:

• D[3,2]- média de área de superfície – Diâmetro médio de Sauter
• D[4,3]- média de volume ou massa – Diâmetro médio de De Brouckere

  Essas médias são semelhantes ao momento de inércia e introduzem termos lineares relacionados a diferentes diâmetros (abaixo, como a área de superfície está correlacionada com d3 e volume e massa com d4).

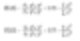
  Essas fórmulas indicam que os pontos centrais das distribuições de frequência (área de superfície ou volume/peso) giram. De fato, eles são cada um o centro de gravidade da distribuição. A vantagem dessa abordagem de cálculo é clara – a fórmula não inclui a contagem de partículas, portanto, o cálculo das médias e distribuição não requer conhecimento sobre o número complexo de partículas. A difração a laser inicialmente calcula contribuições baseadas em termos de volume, e por isso, D[4,3] é claramente relatado.

Diferentes técnicas de medição, diferentes resultados

  Se usarmos um microscópio eletrônico com uma grid para medir as partículas que queremos, somamos ou dividimos pela contagem das partículas para obter o resultado médio. Nós–