Notas Técnicas de Reologia – Entendendo a Correlação entre Reologia e Parâmetros de Partículas1



Download



Entendendo a Correlação entre Reologia e Parâmetros de Partículas 

  As propriedades de materiais particulados são influenciadas tanto pela distribuição de tamanhos quanto pelo potencial zeta (medida da carga das partículas). Ambas afetam a reologia de materiais de revestimento.  Os resultados dos testes cobrem diferentes tipos de revestimentos sob essas influências, e a reologia foi medida com o reômetro Malvern Bohlin Gemini. O tamanho das partículas e o potencial zeta foram medidos com o Malvern Mastersizer 2000 e o Malvern Zetasizer Nano ZS, respectivamente.

  Os exemplos utilizados neste documento consideram condições muito gerais na maioria dos casos, e a teoria pode ser amplamente aplicada a sistemas de revestimento.

  A “fluidez” de um material é expressa pela sua viscosidade ou resistência ao fluxo. Quando se fala em viscosidade de um material específico, é importante perceber que a viscosidade não se refere apenas a um único valor, mas é apresentada como uma função da tensão de cisalhamento.

  A tensão de cisalhamento fornece um índice de deformação do material sob pequenas tensões de cisalhamento abaixo de 1 s-1 e altas tensões de cisalhamento acima de 100 s-1.

  A Tabela 1 resume o processo para materiais de revestimento e o respectivo intervalo de velocidade de cisalhamento.

  Quando consideramos a velocidade de cisalhamento, os materiais utilizados em revestimentos seguem as seguintes categorias:
– Adensamento por cisalhamento (o fenômeno em que a viscosidade aumenta com o aumento da velocidade de cisalhamento);
– Newtoniano (fenômeno em que mantém viscosidade constante em todas as velocidades de cisalhamento);
– Afinamento por cisalhamento (o fenômeno em que a viscosidade diminui com o aumento da velocidade de cisalhamento);

Relação entre Tamanho de Partícula e Reologia

  A primeira consideração é a viscosidade dos adesivos de pressão sensíveis a temperatura (PSA: Pressure-Sensitive Adhesives), que aderem com baixa pressão em baixas temperaturas. No caso de partículas de látex, existem dois tamanhos diferentes. Como mostrado na Fig 1, conforme o tamanho das partículas aumenta, a viscosidade do PSA diminui significativamente.

  É importante perceber que isso é apenas resultado da mudança no tamanho médio das partículas. A fração volumétrica (ou massa de látex adicionada ao PSA) é constante. Para uma dada massa de látex, o número de partículas será determinado pelo tamanho, ou seja, haverá mais partículas de 175 micrometros do que de 750 micrometros.

  Essas interações de partículas são gerais e em materiais maiores as interações são menores; essas podem ser interações mecânicas ou elétricas/químicas. Portanto, partículas menores terão mais partículas no mesmo volume e mais interações.

  Considerando as interações como uma estrutura em pequena escala, isso é medido como um aumento de viscosidade. A velocidade de cisalhamento pode ser considerada um fator de deformação, e uma baixa velocidade de cisalhamento causará menos deformação do que uma alta. Portanto, velocidades de cisalhamento baixas causadas por forças fracas diferem de velocidades de cisalhamento altas causadas por forças fortes. Fig 1 também mostra que a maior diferença de viscosidade é vista em baixas velocidades de cisalhamento, devido a interações de partículas que são fracas e quebram facilmente.

  Como resultado, esses dois sistemas apresentam viscosidade semelhante em altas velocidades de cisalhamento, onde há menos interação de partículas.

  Quando pensamos em tintas à base de resina (tinturas que usam talco como carga) no sistema, a viscosidade variará dentro do sistema. Na Fig 2, a tinta pura exibe viscosidade típica newtoniana. A resina adicionada é um material relativamente duro, então interações entre essas macromoléculas resultam em grande viscosidade, que resiste ao cisalhamento devido a emaranhamentos de polímeros e que manifesta o menor afinamento por cisalhamento possível.

  No caso do talco com partículas de 19 micrometros, as partículas maiores têm interações relativamente menores, apresentando inicialmente uma tendência newtoniana de viscosidade, ligeiramente crescente. No entanto, com partículas menores de 5 micrometros, devido ao maior número de partículas, observa-se um aumento acentuado da viscosidade. Como mencionado anteriormente, essas interações de partículas são geralmente fracas. Por essa razão, o afinamento por cisalhamento se manifesta como maior viscosidade em baixas velocidades de cisalhamento.

Efeito da Fração de Volume e Distribuição

  Até o momento, discutimos a fração volumétrica constante de cargas. Basicamente, uma quantidade fixa de partículas foi introduzida no sistema. Aumentar simplesmente a fração de partículas não altera a viscosidade medida por um viscosímetro. No entanto, ao realizar medições de reologia na prática, essa relação entre viscosidade e velocidade de cisalhamento requer mais detalhes informativos. Fig 3 mostra que a viscosidade em várias velocidades de cisalhamento aumenta à medida que a fração volumétrica das partículas na tinta aumenta. Contudo, vemos também mudanças na fluidez.

  Geralmente, em baixas frações volumétricas (abaixo de 40%), o número de partículas no sistema é tão baixo que elas não interagem significativamente, mantendo as características newtonianas. Em torno de 50%, o número de partículas leva a fortes interações, aumentando a viscosidade. Como discutido anteriormente, essas interações são fracas, sendo descritas por estruturas que se rompem a altas velocidades de cisalhamento, resultando em afinamento por cisalhamento.

  Sistemas com frações volumétricas superiores a 60% têm interações evidentemente maiores, exibindo alta viscosidade mesmo em baixas velocidades de cisalhamento e comportamento de afinamento por cisalhamento. Contudo, dificuldades mecânicas no movimento das partículas nesses sistemas complexos devem ser consideradas. Esse comportamento é especialmente visível em altas velocidades de cisalhamento, manifestando-se como aumento de viscosidade. Aqui, são observados comportamentos de adensamento por cisalhamento ou dilatante.

  A viscosidade dependente da fração volumétrica pode ser expressa pela equação de Krieger-Dougherty. η é a viscosidade da suspensão, ηmedium a viscosidade do solvente base. φ é a fração de volume de sólidos na suspensão, e φm é o valor máximo da fração volumétrica.

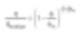
  Além disso, [η] representa a viscosidade intrínseca do solvente, mostrando o valor de 2.5 no caso de partículas esféricas. A equação de Krieger-Dougherty pode variar em função das propriedades das partículas mesmo em frações volumétricas constantes. Nesta situação, é o tamanho das partículas e o intervalo de distância que afetam diretamente o valor máximo da fração volumétrica (ou empacotamento). Para sistemas de partículas esféricas monodispersas, o máximo teórico é de cerca de 64%. Entretanto, esse valor aumenta efetivamente nos arredores das partículas com fluxo (ou seja, quando a razão volumétrica é pequena). Isso pode ser entendido pelo fato de que as partículas menores funcionam eficientemente como lubrificantes no movimento de partículas maiores.

  Fig 4 mostra que isso pode resultar em descobertas interessantes. Ela revela que, em uma fração fixa de volume, a viscosidade de sistemas polidispersos compostos por partículas grandes e pequenas pode ser menor que as viscosidades individuais. Existem dois efeitos opostos acontecendo: um é o número de partículas interagentes, afetado pelo tamanho das partículas; o outro é o efeito da polidispersidade.

  Nos sistemas de revestimento, aumentar simplesmente a polidispersidade ou a quantidade de aditivos garante que, mesmo após a adição de cargas ou pigmentos, a viscosidade permaneça inalterada sob uma dada condição.

  O efeito da polidispersidade deve ser considerado quando um fornecedor substitui os aditivos de revestimento porque os fornecedores não afetam a distribuição, já que utilizam o mesmo tamanho de partícula. Desse modo, a reologia não apresenta mudança. Por exemplo, quando se mede com o Mastersizer 2000, é possível avaliar tanto o tamanho quanto a distribuição do tamanho das partículas.