Compreensão e Princípios da Análise de Tamanho de Partículas com Análise a Laser

Princípios Básicos da Análise de Tamanho de Partículas

O que é uma Partícula?

Perguntar isso pode parecer uma questão ignorante, mas é um fundamento básico para várias técnicas de análise de tamanho de partículas. O processo de dispersão e a forma do material tornam-se mais complexos na análise de tamanho de partículas em comparação ao início.

Problema do Tamanho das Partículas

Imagine que alguém lhe entregue uma caixa de fósforos e peça para você dizer o tamanho dela.  

Você provavelmente responderia que a caixa de fósforos mede 20*10*5mm.  

É improvável que você possa responder exatamente que o tamanho da caixa de fósforos é 20mm, pois isso representa apenas uma perspectiva em relação ao tamanho. Por isso, você não pode descrever uma caixa de fósforos tridimensional com uma única dimensão.  

Esta situação fica ainda mais complicada em partículas de areia ou pigmentos de tinta, que têm formas complexas.  

 

Se eu fosse um gerente de controle de qualidade, provavelmente gostaria de ter um único número para descrever as partículas — por exemplo, saber se o tamanho médio do produto final aumentou ou diminuiu. Este é o problema fundamental na análise do tamanho das partículas: como podemos expressar um objeto tridimensional com apenas um número? 

 


A Figura 1 mostra algumas partículas de areia. Qual é o tamanho delas? 

 

Esferas Equivalentes 

 Existe uma esfera que pode ser expressa com um número único. Se dissermos que é uma esfera de 50μm, isso pode ser precisamente expresso. Não se pode exprimir o lado ou a diagonal de um cubo de 50μm de maneira precisa. 

 

Caixas de fósforos com várias características podem ser expressas com um único número. Por exemplo, o peso em relação ao volume ou à área de superfície é um número específico. Se tivermos uma técnica para medir o peso de uma caixa de fósforos, podemos converter seu peso no peso de uma esfera equivalente. 

 

Importante lembrar que  

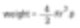
E então calcula-se um número específico (2r) para o diâmetro de uma esfera com o mesmo peso da caixa de fósforos. Este é o conceito de esfera equivalente. 

 

Medimos certas propriedades de partículas e assumimos que são esferas. Assim, obtemos um número específico (diâmetro da esfera) para representar as partículas. 

 

Apesar de mais preciso para controle, o fato de não requerer ser expresso em três ou mais números está associado à incapacidade de representar corpóreos tridimensionais desta forma. 

 

É possível conhecer efeitos interessantes relacionados à forma do objeto, ilustrados por cilindros semelhantes a esferas. (Fig.2)  

 

Contudo, se o formato ou tamanho do cilindro mudar, o volume/peso será diferente. Pelo modelo de esfera equivalente, poderemos, no mínimo, dizer se o objeto aumentou ou diminuiu de tamanho. 

Cilindro de 100 x 20μm e Diâmetro da Esfera Equivalente 

 

Vamos imaginar que o diâmetro do cilindro é D1=20μm com 100μm de altura. Existe uma esfera de diâmetro D2 com o mesmo volume do cilindro. Podemos calcular o diâmetro como mostrado. 

 

Volume do cilindro  

 

Volume da esfera  

 

 

X representa o raio do volume. 

O diâmetro da esfera equivalente de um cilindro de 100μm de altura e 20μm de diâmetro é cerca de 40μm. A tabela abaixo representa os diâmetros esféricos de cilindros com várias proporções. A última linha seria uma representação típica de uma grande partícula de argila em forma de disco. Como tem 20μm de altura e 0,2μm de espessura, na maioria dos casos a consideração das dimensões não é necessária. 

 

Ao considerar instrumentos para medir o volume das partículas, talvez recebamos um valor em volta de 5μm. Neste caso, deve-se usar outra técnica que pode contestar esta resposta. 

 

Da mesma forma, todos esses cilindros terão a mesma aparência que um filtro de 25μm, período quando afirmamos que ‘todas as substâncias são menores que 25μm’. Como cada cilindro possui valor diferente, a difração a laser pode apresentar resultados diversos. 

Diversas Técnicas de Medição

Claramente, se observarmos as partículas através de um microscópio, verá uma projeção bidimensional e poderá medir diversos diâmetros característicos. Se quisermos utilizar o comprimento máximo da partícula como nosso tamanho, podemos chamar esta partícula de esfera de máximo diâmetro. 

 

Da mesma forma, utilizando o diâmetro mínimo ou valores como o diâmetro de Feter, obteremos outra resposta sobre o tamanho das partículas. É importante saber que cada técnica mede uma diferente propriedade da partícula (comprimento máximo, mínimo, volume, área de superfície, etc.). Assim, medidas seletivas podem resultar em respostas diferentes das outras técnicas. 

Fig 3 mostra várias soluções possíveis para descrever um grão de areia. Nenhuma dessas técnicas está errada — todas medem diferentes propriedades da partícula. É análogo a medir uma caixa de fósforos em centímetros ou polegadas (você mede o comprimento, eu meço a largura!). 

 

Assim, podemos comparar apenas medições feitas sob as mesmas condições em pó. Isso sinaliza que grãos como areia não têm um tamanho padrão. O padrão deve ser tal que permita comparação entre diferentes tecnologias de medição. 

Porém, cada técnica pode oferecer um valor padrão da partícula e isso permitirá a comparação de tecnologias e dispositivos usados. 

D[4,3]

Considere três esferas com dimensões de 1, 2 e 3 unidades. Como calcularíamos o tamanho médio entre essas três partículas? Primeiro, diríamos que seria 2. Como chegamos a esse número? 


Somamos todos os valores e dividimos pelo número total de partículas.    

 

 

Este é o cálculo médio (mais especificamente, a média numérica). Pode-se expressar por meio de equações a quantia de partículas. 

 

 

Em termos matemáticos é chamado de D[1,0].  

Isto porque a fração no topo da equação possui poder (d1) e a fração inferior não possui poder (d0). Se eu fosse engenheiro de catálise, consideraria tais esferas a base de área de superfície, uma vez que uma maior área de superfície resulta em maior reatividade catalítica. 

 

A área de superfície de uma esfera é . Assim, ao comparar pela área de superfície, é necessário calcular o quadrado dos diâmetros e dividi-los pelo número de partículas. Para retornar ao diâmetro médio, retire a raiz quadrada do quadrado. 

 

Novamente, essa é a média (de superfície). A razão para a aparição do número de partículas na equação inferior nas equações. Somamos os quadrados dos diâmetros. Por essa razão, o termo matemático é D[2,0]. No caso de eu ser um quimico, preferiria comparar as esferas no sentido de peso. A seguinte equação mostra o peso de uma esfera. 

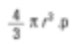
Devemos também entender a dimensão cúbica dividida pelo número de fatores e retirar a raiz cúbica para encontrar o diâmetro médio. 

＆nbsp;