Principes de base de l’analyse granulométrique-2

Télécharger



Distribution en nombre et en volume 

 

  L’exemple ci-dessus provient de New Scientist (31 octobre 1991). Il y a un grand nombre déterminé par l’homme qui tourne autour de la Terre dans l’espace, et également dans leurs orbites régulières. Les scientifiques ont également classé des groupes sur la base de leur taille. Si nous examinons le troisième paragraphe ci-dessus, nous pouvons déduire que 99,3% des particules sont incroyablement petites. Ceci est une évaluation basée sur les données numériques. Cependant, si nous examinons le quatrième paragraphe, nous pouvons déduire que pratiquement tous les objets mesurent entre 10 et 1000 cm. C’est la masse de tous les objets. Les distributions en nombre et en masse sont très différentes et nous devons noter que les conclusions tirées peuvent être différentes selon la distribution utilisée. Ni une distribution n’est exacte. Les données sont simplement examinées d’une autre manière. Par exemple, si nous fabriquons une combinaison spatiale, nous saurons qu’il est facile d’éviter 7000 grands objets et nous devrions surveiller 99,96% des cas. Cependant, l’aspect le plus important d’une combinaison spatiale est de protéger contre les 99,3% de petites particules selon le nombre. Si nous calculons la moyenne des distributions dans le tableau, nous devrions savoir que la moyenne en nombre est d’environ 1,6 cm et la moyenne en masse est d’environ 500 cm. – Cela diffère donc considérablement.

Conversion entre les distributions en nombre, longueur, volume/masse

  Si nous déterminons des particules par microscopie électronique, nous calculons la taille moyenne en nombre-longueur D[1,0] comme expliqué précédemment (d’autres techniques donnent des moyennes différentes). Si ce que nous recherchons est la taille moyenne en masse ou en volume, nous devons convertir la moyenne en nombre en moyenne en masse. Mathématiquement, cela est facilement réalisable, mais nous devons examiner le résultat d’une telle conversion.

  Supposons qu’une technique de mesure électrique présente une erreur de +/-3% dans la taille moyenne. Lorsque nous convertissons la taille moyenne en nombre en taille moyenne en masse, l’erreur en masse est une fonction en cube du diamètre, devenant alors un cube de la valeur finale ou +/-27%.

 











  Cependant, si nous calculons des distributions de masse ou de volume par diffusion laser, la situation sera différente.

  En mesurant un échantillon stable dans des conditions de recirculation par dissolution, nous pouvons obtenir une moyenne en volume reproductible de +/-0,5%.

  Si nous transformons maintenant cette moyenne en volume en moyenne en nombre, l’erreur ou la moyenne en nombre sera le cube de la racine de 0,5% ou même inférieure à 1,0%.

  En fait, si nous voulons une distribution de volume ou de masse en utilisant un microscope électronique, ignorer ou perdre une particule de 10μ équivaut à ignorer ou perdre mille particules de 1μ. Par conséquent, nous devons prendre en compte le grand risque de la conversion entre elles.

  Les deux logiciels DOS et Windows de Malvern Sizers calculeront les différents diamètres. Cependant, nous devons être très prudents lors de cette mesure. D’autres méthodes (significations) peuvent être transformées différemment selon les formules suivantes (formules de transformation de Hatch-Choate-Ref.7).

 

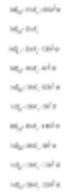
Mesure et diamètre induit

  Nous avons observé que la technique de diffraction laser Malvern produit une distribution de volume pour l’analyse des données d’énergie lumineuse. (Notez que la distribution de l’aire examinée par l’analyse Fraunhofer a été supposée.) Cette distribution de volume peut être transformée en nombre ou en longueur de diamètre comme indiqué ci-dessus.

  Cependant, dans toute technique analytique, nous devons savoir quel diamètre moyen est effectivement mesuré par la machine, et quel diamètre est réellement calculé ou dérivé du premier diamètre mesuré.

  D’autres méthodes pourront dériver d’autres diamètres à partir de quelques diamètres déjà mesurés. Par exemple, le microscope mesurera D[1,0] et d’autres diamètres pourront être obtenus à partir de là.

  Nous pouvons faire davantage confiance aux diamètres mesurés plutôt qu’aux diamètres calculés. En fait, dans certains exemples réels, s’engager sur des caractéristiques dérivées (calculées) peut être très risqué. Par exemple, le tableau d’analyse de Malvern nous présente la surface spécifique (m/cc ou m/gm).

  Nous ne devrions pas accepter le tableau sans réserve. – En fait, si ce que nous voulons vraiment est la surface spécifique d’un matériau, nous devrions utiliser des techniques spécifiques qui mesurent la surface telle que la porosimétrie au mercure ou la méthode de B.E.T.

Quel nombre utiliser ?

  Un autre principe déjà connu est que l’on mesure des propriétés différentes (ou tailles) des particules et qu’il s’agit d’utiliser les données de nombreuses manières différentes pour obtenir des résultats moyens différents (D[4,3], D[3,2], etc.). Alors, pourquoi devrait-on utiliser des nombres ?

  Considérons un exemple simple avec des diamètres de sphères de 1 et 10 unités. Supposons que nous fabriquons de l’or. Si nous calculons un diamètre moyen simple en nombre, il est donné par :

 

 

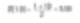
  Donc, nous pourrions supposer que la taille moyenne des particules dans le système est de 5.50 unités. Cependant, nous devrions nous rappeler que si nous fabriquons de l’or, nous devrions être intéressés par le poids du matériau.

  Par exemple, si nous connaissons la tendance du processus, nous ne serons pas intéressés par le fait qu’il y ait 3,5 millions de particules. Plutôt, nous voudrions savoir s’il y a 1 kg ou 2 kg d’or.

  En connaissant que la moyenne des masses est une fonction en cube du diamètre, nous réalisons que la sphère de diamètre 1 unité possède une masse de 1 unité, et une sphère de diamètre 10 unités possède une masse de 10=1000 unités.

  Cela signifie que la plus grande sphère représente 1000/1001 de la masse totale du système. Si nous fabriquons de l’or, nous pourrons jeter la sphère de 1 unité car nous perderions ainsi moins de 0.1% de la masse totale du système. Par conséquent, la moyenne en nombre causerait certainement un biais par rapport à la masse dérivée du système. Ceci est plus avantageux sur D[4.3].

  Dans l’exemple de nos deux sphères, le moment moyen en masse ou en volume serait calculé comme dans l’équation suivante.

 

 

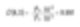
  Cette valeur montre où la masse du système se situe et devient importante pour les ingénieurs en processus chimique.

  Mais supposons que nous fabriquons des wafers de silicium ou d’arséniure de gallium dans une salle blanche. Ici, si une particule se trouve sur un wafer, cela pourrait provoquer un défaut. Dans cet exemple réel, le nombre ou la concentration de particules est très important, car une particule signifie un défaut et nous devons utiliser des techniques qui peuvent mesurer directement le nombre spécifique ou la concentration des particules. Essentiellement, cela est différent entre le nombre total de particules et la taille des particules. Pour le nombre total, nous comptons et enregistrons chaque particule. La taille est moins importante. Nous avons besoin d’échelles de taille à certains seuils (mentionné dans 8). Du point de vue de la taille, les particules de tailles spécifiques sont moins pertinentes par rapport à la contribution de la taille ou à la taille des particules et nous avons besoin de plus de bandes de tailles.

  En mesurant une dose d’inhalateur pour un patient asthmatique, à la fois la concentration du médicament et la contribution de la taille des particules sont importantes.

Moyenne, médiane, mode – Statistiques de base 

 

Moyenne

  C’est la moyenne arithmétique de certaines données. Il existe de nombreuses moyennes qui peuvent être calculées pour les particules. (Voir la section D[4,3], etc.)

Médiane

  C’est la valeur de la taille de la particule qui divise exactement la population en deux parties égales. Par exemple, 50% de la distribution au-dessus et 50% au-dessous de cette valeur.

Mode

  La valeur, comme le point le plus élevé d’une courbe de fréquence, est la valeur la plus fréquente de la distribution. Considérant que cette distribution est une distribution normale ou gaussienne. Moyenne, médiane, mode sont exactement à la même position. Voir la Fig. 4. Mais supposons que cette distribution ait deux modes comme le montre le diagramme 5 (bimodale).

 

 

  Le diamètre moyen serait approximativement au milieu des deux distributions sur le graphique si elles étaient visibles. Notez qu’il n’y a pas de particule de cette taille moyenne. Le diamètre médian serait à peu près à 1% du côté de la distribution supérieure car cela divise exactement les deux distributions. Le mode serait le sommet de la distribution supérieure car c’est la valeur la plus fréquente du diamètre.



  Cet exemple démontre qu’il n’y a aucune raison que la moyenne, la médiane et le mode, biaisés par la symétrie de la distribution, doivent être idéalement ou encore même égaux.