Principe Fondamental de l’Analyse Granulométrique-1

Téléchargement



Principe Fondamental de l’Analyse Granulométrique 

Qu’est-ce qu’une particule?

  Poser cette question est très naïf. Cependant, cela constitue une base fondamentale pour diverses techniques d’analyse de la taille des particules. Le processus de dispersion et la forme des matériaux deviennent de plus en plus compliqués pour l’analyse de la taille des particules.

Problème de la taille des particules

  Supposons que l’on vous donne une boîte d’allumettes et que l’on vous demande de déterminer sa taille. Vous diriez peut-être qu’elle mesure 20*10*5mm. Vous ne pourriez pas répondre précisément « La taille de la boîte d’allumettes est de 20mm », et ceci est juste une façon de voir la question de la taille. Ainsi, il est évident que vous ne pouvez pas décrire une boîte d’allumettes tridimensionnelle en se basant seulement sur une dimension unique. Cette situation devient encore plus complexe lorsqu’on considère des formes plus compliquées comme des particules de sable ou des pigments dans une boîte de peinture. Si j’étais un manager Q.A., je souhaiterais avoir un chiffre unique pour décrire une particule – par exemple, savoir si la taille moyenne d’un produit récemment fabriqué a augmenté ou diminué. Cela pose la question fondamentale de l’analyse de la taille des particules – comment représentons-nous un objet tridimensionnel avec un seul chiffre?

Sphères équivalentes

  Il existe une sphère qui peut être exprimée par un seul chiffre. Lorsque nous disons qu’il s’agit d’une sphère de 50μm, cela devient précisément exprimable. On ne peut exprimer ni les arêtes ni les diagonales d’un cube de 50μm de manière aussi précise. Une boîte d’allumettes avec de nombreuses caractéristiques peut être exprimée par un seul chiffre. Par exemple, le poids en relation avec le volume et la surface est un chiffre particulier. Ainsi, si vous avez une technique pour peser la boîte d’allumettes, vous pouvez convertir son poids en celui d’une sphère.

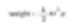
  Il est important de calculer une valeur spécifique (2r) pour le diamètre d’une sphère qui a le même poids qu’une boîte d’allumettes. C’est le principe des sphères équivalentes. Nous mesurons la propriété d’une particule et supposons qu’il s’agit d’une particule sphérique. Ainsi, nous obtenons une valeur unique (diamètre de la sphère) pour représenter la particule.

   Cela indique que même si pour des raisons de contrôle il pourrait être plus exact d’utiliser trois chiffres ou plus pour représenter un objet tridimensionnel, il n’est pas nécessaire de le faire.

   On peut voir des effets intéressants dépendant de la forme d’un objet, illustrés par exemple avec un cylindre en forme de sphère.

  Cependant, si la forme ou la taille du cylindre change, le volume/poids changera également. Et comme nous utilisons le modèle sphérique équivalent, au minimum nous pouvons dire qu’il a rétréci ou grandi.

Diamètre sphérique équivalent (Equivalent spherical) d’un cylindre 100 x 20μm

  Imaginons que le diamètre du cylindre soit D1=20μm pour une hauteur de 100μm. Il existe une sphère ayant le même volume que le cylindre et ayant un diamètre D2. Nous pouvons calculer ce diamètre comme suit.

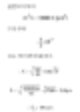
  Le volume du diamètre sphérique d’un cylindre de 100μm de hauteur et 20μm de diamètre est d’environ 40μm. Le tableau ci-dessous représente le diamètre sphérique de cylindres de différents rapports. La dernière ligne représenterait une particule typique en forme de disque de grande taille constituée d’argile. Comme elle a une hauteur de 20μm et une épaisseur de 0.2μm, généralement sa dimension n’est pas considérée. Concernant un outil qui mesure le volume, nous pourrions obtenir une réponse d’environ 5μm. Donc, nous devons utiliser différentes techniques en cas de contestation de cette réponse.

  De plus, tous ces cylindres peuvent apparaître de même taille que les filtres de 25μm et on pourrait donc dire que “tous les matériaux sont en dessous de 25μm”. Ces cylindres peuvent apparaître différemment en diffraction laser, car ils ont chacun des valeurs différentes.

Diverses techniques de mesure

  De toute évidence, si nous observons une particule au microscope, nous pouvons voir ce qui est projeté en 2D et il existe certains diamètres de particules caractérisables et mesurables. Si nous acceptons la longueur maximale de la particule et l’utilisons comme notre mesure de taille, nous pouvons dire qu’il s’agit d’une particule sphérique ayant la plus grande dimension. De même, si nous utilisons des mesures telles que le diamètre minimal ou le diamètre de Feter, cela nous fournira une autre réponse concernant la taille de la particule. Pour cette raison, nous devons savoir que chaque technique peut mesurer différentes propriétés d’une particule (longueur maximale, longueur minimale, volume, surface, etc.) et donc, à mesure souhaitée, elle montrera des résultats différents des autres techniques.

  Fig 3 montre différentes solutions possibles qui peuvent permettre de décrire un grain de sable. Chacune des techniques n’est pas incorrecte – elles mesurent toutes différentes propriétés d’une particule. C’est comme si vous mesuriez une boîte d’allumettes en utilisant le système cm tandis que je mesure sa largeur!

  De cette manière, nous ne pouvons que comparer ce qui est mesuré avec la même technique. Cela signifie qu’il n’existe pas de taille standard pour une particule de sable. Les normes doivent être sphériques lorsque comparé entre les techniques. Cependant, nous pouvons obtenir une taille standard de particule pour chaque technique, ce qui permettra de comparer les équipements utilisant cette technique.

D[4,3] etc.

  Imaginez avoir trois sphères de tailles 1, 2, et 3. Quelle serait la taille moyenne des trois particules? Initialement, on pourrait dire 2. Comment est-ce que l’on obtient cette réponse? Ajoutez toutes les valeurs et divisez par le nombre total de particules.

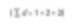
 C’est la moyenne arithmétique (plus précisément, la moyenne arithmétique linéaire). Le nombre de particules peut être représenté par une équation.

  Mathématiquement, nous l’appelons D[1,0]. La raison est que le numérateur de l’équation ci-dessus a des termes en diamètre (d1) et que le dénominateur n’en a pas (d0). Or, si je suis ingénieur en catalyse, je voudrais comparer ces sphères sur la base de leur surface, car une surface plus grande implique une plus grande réactivité du catalyseur. L’expression de la surface d’une sphère est 4πr². Par conséquent, si l’on compare sur la base de la surface, on doit s’assurer de calculer le carré des diamètres divisés par le nombre de particules. Et pour revenir au diamètre moyen, on prend la racine carrée.

  Ceci est encore une moyenne arithmétique (moyenne d’aire projetée). La raison en est que le nombre de particules figure dans l’équation. On additionne tous les carrés des diamètres. Ainsi, ce terme est mathématiquement appelé D[2,0] – le numérateur de l’équation a un carré tandis que le terme du dénominateur n’est pas présent. Si je suis un chimiste, je voudrais comparer les sphères basées sur le poids de base. L’expression pour le poids est comme suit.

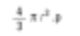
  Et nous devons savoir que les dimensions divisées par le nombre de particules et la racine cubique sont prises pour revenir au diamètre moyen.

  Encore une fois, cela se divise par une moyenne arithmétique (moyenne pondérée par volume ou pondérée par poids). La raison est que le nombre de particules est présent dans l’équation. Cela s’exprime mathématiquement comme D[3,0].

  Le problème avec les moyennes simples D[1,0], D[2,0], D[3,0] réside dans le fait que le nombre de particules est adressé dans la formule. Cela nécessite souvent le besoin de calculer de nombreux particules. Les particules contrôlées, telles que celles utilisées pour la pollution, le contrôle, ou la propreté sont généralement comptées seulement lorsqu’elles se produisent à de faibles quantités (par exemple ppm ou ppb). Si tous les 1g de Silice (densité 2.5) mesuraient 1μm, cela montrerait qu’il y a environ 760*10^9 particules à travers un calcul simple.

Donc, il est nécessaire de compléter le concept moyen instantané pour éviter toute confusion. Les deux moyennes les plus significatives sont les suivantes :

• D[3,2]- Moyenne aréale – diamètre moyen de Sauter
• D[4,3]- Moyenne volumique ou pondérée – diamètre moyen de De Brouckere

  Ces moyennes sont similaires aux moments d’inertie et introduisent un terme linéaire lié à un autre diamètre. (Comme ci-dessous la surface est corrélée à d3 et le volume et la masse à d4.)

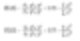
  Cette formule montre que le centre de distribution de la fréquence (surface ou volume/masse) pivote. En réalité, ce sont simplement le centre de gravité de chaque distribution. L’avantage de ce calcul est évident – car les formules n’incluent pas le nombre de particules, et les calculs peuvent être effectués concernant des distributions sans avoir besoin de connaître le nombre complexe de particules. La diffraction laser commence par calculer la contribution basée sur le terme de volume, et il est rapporté aiguillant de D[4,3].

Différentes techniques de mesure donnent différents résultats

  Si nous utilisons un microscope électronique à balayage pour mesurer le diamètre d’une particule, nous diviserons ou ajouterons simplement par le nombre de particules pour obtenir une moyenne.