Notes techniques sur la rhéologie – Comprendre la corrélation entre la rhéologie et les paramètres des particules1



Télécharger



Comprendre la corrélation entre la rhéologie et les paramètres des particules 

 Les propriétés des microparticules sont influencées à la fois par la distribution de taille et le potentiel zêta (charge des particules), tous deux ayant un impact sur la rhéologie des substances enduites. Les résultats ont couvert plusieurs types de revêtements différents, et la rhéologie a été mesurée avec un rhéomètre Malvern Bohlin Gemini. La taille des particules et le potentiel zêta ont été mesurés respectivement avec le Malvern Mastersizer 2000 et le Malvern Zetasizer Nano ZS.

 L’exemple présenté dans ce document considère des conditions très courantes, et la théorie peut être largement appliquée au système de revêtement.

 Le « flowability » d’une substance est représenté par sa viscosité ou sa résistance à l’écoulement. Quand on parle de la viscosité d’une substance spécifique, il est important de comprendre que la viscosité n’est pas seulement un seul chiffre mais qu’elle est exprimée en tant que fonction de la contrainte de cisaillement.

 La contrainte de cisaillement fournit un indicateur de la déformation que subit la matière sous une contrainte de cisaillement basse (1s-1) ou élevée (100s-1).

 La table 1 résume les processus concernant les matériaux de revêtement et les gammes de vitesses de cisaillement qui en résultent.

 En termes de réflexion sur la vitesse de cisaillement, les matériaux utilisés dans le revêtement adhèrent aux catégories suivantes.

– Épaississement au cisaillement (augmentation de la viscosité avec l’augmentation de la vitesse de cisaillement);
– Newtonien (viscosité constante à toutes les vitesses de cisaillement);
– Fluidification par cisaillement (diminution de la viscosité avec l’augmentation de la vitesse de cisaillement);

Relation entre granulométrie et rhéologie

La première chose à prendre en compte est la viscosité des adhésifs sensibles à la pression (PSV) ; ceux qui adhèrent au substrat sous faible pression même à température ambiante. Les particules de latex examinées avaient deux tailles différentes. Comme on peut le voir sur la Fig 1, plus la taille des particules est grande, plus la viscosité du PSA diminue sensiblement.

Nous savons que ce résultat est dû uniquement aux changements de la taille moyenne des particules. Le pourcentage volumique (ou masse de latex ajouté à le PSA) est fixé. Après introduction de la masse donnée du latex, le nombre de particules dépendra de leur taille. Un latex de 175 microns comportera plus de particules qu’un de 750 microns.

Cela constitue une interaction générale entre particules. Dans un matériau plus gros, peu d’interaction existe, qu’elle soit mécanique ou électrostatique/chimique. Par conséquent, dans le même pourcentage volumique, les petites particules présenteront plus d’interactions.

Considérant les interactions comme des structures compactes, une viscosité accrue peut être constatée. La vitesse de cisaillement peut être considérée comme un facteur de déformation : à basse vitesse il y a peu de déformation par rapport à une vitesse élevée. C’est pourquoi la Fig 1 montre que la viscosité la plus marquée se trouve à basse vitesse, avec des interactions faibles qui se brisent facilement.

Ainsi, ces deux systèmes montrent une viscosité similaire à haute vitesse de cisaillement en raison de l’interaction réduite entre les particules.

Dans le cas des encres à base de résine (utilisant du talc comme charge), la viscosité change dans le système. Fig 2 montre que l’encre pure présente un comportement newtonien typique. La résine ajoutée est un matériau assez résistant, et l’interaction entre ces polymères peut entraîner une grande viscosité, avec un cisaillement faible dû à un entrelacement polymère limitant les mouvements.

Dans le cas de particules de talc de 19 microns, la taille des particules réduit l’interaction, offrant au départ une tendance newtonienne douce au niveau de la viscosité. Cependant, lorsque des particules plus petites de 5 microns sont ajoutées, l’augmentation du nombre de particules augmente considérablement la viscosité. Encore une fois, les interactions de particules sont généralement faibles, ce qui se traduit par une fluidification par cisaillement observée à basse vitesse.

Impact du volume et du degré de dispersion

Jusqu’à présent, nous avons discuté d’un certain pourcentage volumique des charges. Isaient fondamentalement des particules fixées dans le système. Augmenter simplement la fraction volumique des particules conduira à une augmentation de la viscosité. Cependant, mesurer réellement la rhéologie introduit la relation entre la viscosité et la vitesse de cisaillement. Fig 3 montre que la viscosité de l’encre à différentes vitesses de cisaillement augmente avec le volume de particules, mais la fluidité change également.

Généralement, à une faible fraction volumique (<40%), le nombre de particules dans le système est si faible qu'il n'y a pas d'échanges; la propriété newtonienne est maintenue. À environ 50%, une interaction forte cause une augmentation de la viscosité. Comme discuté auparavant, ces interactions sont faibles et entraînent une fluidification par cisaillement qui brise ces structures.

Avec des fractions volumiques élevées (60% et plus), il y aura une réaction intensive, une haute viscosité à basse vitesse et une tendance au cisaillement qui se manifeste plus distinctement à haute vitesse. Ceci s’apparente à une épaississement au cisaillement ou à une propriété dilatante.

La viscosité selon le volume peut être présentée par l’équation de Krieger-Dougherty. η est la viscosité de la suspension, et ηmedium celle du solvant de base. φ représente le pourcentage volumique de solide dans la suspension et φm en est le maximum.

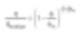
[η] représente la viscosité intrinsèque, avec une valeur de 2,5 pour les particules sphériques. Selon l’équation de Krieger-Dougherty, la distribution et la plage de taille des particules, qui influencent le volume maximum, peuvent modifier la performance des particules à une fraction volumique constante. Dans un système avec des particules sphériques bien dispersées, le volume maximum est d’environ 64%. Ceci peut également être augmenté efficacement à faible fraction volumique grâce à l’effet de flux, qui réduit la viscosité, notamment par l’action de lubrification des petites particules permettant le mouvement des plus grosses.

Fig 4 montre les effets intéressants de ce phénomène; la viscosité d’un système polydisperse composé de grandes et de petites particules peut être inférieure à celle des composants individuels. Deux effets conflictuels apparaissent, l’un influencé par le nombre de particules interagissant selon la taille et l’autre par l’effet de polydispersion.

Dans les systèmes de revêtement, l’augmentation de la polydispersité ou des additifs permet un maintien de la viscosité, même après ajout de charges ou de pigments. L’effet polydispersité doit être pris en compte lors du remplacement des additifs de revêtement par d’autres fournisseurs. Autrement, la rhéologie reste inchangée avec l’utilisation de la même taille de particules, mesurable avec le système Mastersizer 2000 qui évalue à la fois la taille et la distribution des particules.