Compréhension de l’analyseur granulométrique au laser et principes de l’analyse granulométrique

Principe de base de l’analyse granulométrique

Qu’est-ce qu’une particule?

C’est une question très naïve. Cependant, c’est la base dans diverses techniques d’analyse de tailles de particules. Le procédé de dispersion et la forme des matériaux deviennent plus compliqués que jamais dans l’analyse de tailles de particules.

Problème de taille des particules

Supposons que vous donniez une boîte d’allumettes et que quelqu’un vous demande quelle est sa taille. 

On pourrait répondre que la boîte d’allumettes mesure 20*10*5 mm. 

Il est impossible de dire exactement « la boîte d’allumettes mesure 20 mm », cela représenterait un point de vue parmi d’autres. On ne peut pas décrire une boîte d’allumettes en trois dimensions avec un seul nombre.  

Cette situation devient plus compliquée lorsque la forme est complexe comme pour une particule de sable ou des pigments dans une boîte de peinture. 

 Si j’étais responsable qualité(QA), je voudrais un seul chiffre pour décrire une particule – par exemple pour savoir si la taille moyenne du dernier lot de production augmente ou diminue. C’est la question fondamentale de l’analyse de tailles de particules – comment peut-on représenter un objet tridimensionnel avec un seul chiffre? 

 
La Figure 1 montre des particules de sable. Quelle est leur taille? 

Sphères équivalentes 

Une sphère peut être représentée par un seul chiffre. Si nous parlons d’une sphère de 50 μm, elle peut être représentée avec précision. Mais nous ne pouvons pas le faire pour une arête ou une diagonale d’un cube de 50 μm de diamètre. 

De nombreuses caractéristiques d’une boîte d’allumettes peuvent être représentées par un seul chiffre. Par exemple, la masse associée au volume et à la surface est un chiffre particulier. Donc, si nous avons une technique pour mesurer le poids d’une boîte d’allumettes, nous pouvons le convertir en poids d’une sphère. 

Gardez à l’esprit que nous calculons un chiffre particulier (2r) du diamètre d’une sphère ayant le même poids qu’une boîte d’allumettes. C’est la théorie de la sphère équivalente. 

Nous mesurons la caractéristique d’une particule et supposons que la particule est une sphère. Ainsi nous obtenons un chiffre particulier (diamètre de la sphère) pour représenter la particule. 

Ceci indique qu’il n’est pas nécessaire d’utiliser trois ou plusieurs chiffres lorsqu’on représente une particule en trois dimensions, bien que cela puisse être moins précis pour les objectifs de contrôle que d’utiliser plus de chiffres. 

Ceci démontre des effets intéressants qui dépendent de la forme de l’objet, comme illustré par un cylindre équivalent à une sphère (Fig.2). 

Toutefois, si la forme ou la taille du cylindre change, le volume/poids se modifie aussi. Et dans le modèle de sphère équivalente, nous pouvons au moins dire qu’il est plus grand ou plus petit. 

Diamètre des sphères équivalentes d’un cylindre 100 x 20μm 

Considérons un cylindre de diamètre D1=20μm et de hauteur 100μm. Il existe une sphère de diamètre D2 ayant le même volume que le cylindre. Nous pouvons calculer le diamètre comme suit. 

Le volume du cylindre  

Le volume de la sphère  

X est la valeur du rayon du volume. 

Le diamètre sphérique du volume d’un cylindre de hauteur 100μm et de diamètre 20μm est d’environ 40μm. Le tableau ci-dessous représente le diamètre sphérique de cylindres de différentes proportions. La dernière ligne concerne de grandes particules d’argile typiques en forme de disque. Elles ont une hauteur de 20μm avec une épaisseur de 0,2μm donc généralement on ne considère pas cette dimension. 

En ce qui concerne l’outil pour mesurer le volume d’une particule, nous pourrions obtenir une réponse d’environ 5μm. Par conséquent, pour apprendre à contester cette réponse, vous devrez utiliser une méthode différente. 

De plus, tous ces cylindres peuvent apparaître comme une taille égale au filtre de 25μm en disant que « tout est inférieur à 25μm ». Ces cylindres auront une apparence différente à la diffraction laser car ils ont chacun une valeur différente. 

Différentes techniques de mesure

Évidemment, si vous regardez les particules au microscope, vous observerez des particules projetées en deux dimensions. Vous pouvez ensuite caractériser et mesurer les diamètres des particules. Si nous acceptons la longueur maximale de la particule et utilisons cela comme notre taille, nous pouvons dire que la particule est une sphère ayant la dimension maximale. 

De même, si l’on utilise des quantités telles que des diamètres minimaux ou le diamètre de Feter, cela nous fournira une autre réponse concernant la taille des particules. C’est pour cela que chacune de ces techniques mesure différentes propriétés de la particule (longueur maximale, longueur minimale, volume, surface, etc.). Par conséquent, la mesure sélective produira des résultats différents des autres techniques. 

La Fig.3 illustre plusieurs solutions qui permettent de représenter un grain de sable. Chacune de ces techniques n’est pas incorrecte – elles mesurent toutes différentes propriétés de la particule. C’est comme mesurer une boîte d’allumettes avec des unités de cm ou d’inch (vous mesurez la longueur et moi la largeur !). 

Comme ceci, nous ne pouvons mesurer le même échantillon de poudre qu’avec la même technique, ce qui signifie que pour une particule de sable, aucun standard de taille n’est applicable. Le standard doit être uniforme à partir de comparaisons entre les différentes techniques. Cependant, nous pouvons obtenir des tailles de particules standards pour chaque technique, et nous comparerons ainsi le matériel utilisé avec chaque technique.  

D[4,3]

Supposons que nous ayons trois sphères de dimensions 1, 2, 3 unités. Quelle est la taille moyenne des trois particules? Au départ, on pourrait dire que c’est 2. Comment est-ce que l’on a obtenu ce résultat? Nous additionnons toutes les valeurs et les divisons par le nombre total de particules.    

C’est une moyenne numérique (plus précisément c’est une moyenne de longueur numérique). Le nombre de particules peut être exprimé mathématiquement.  

En termes mathématiques, on l’appelle D[1,0], parce que dans l’équation ci-dessus le terme de diamètre est présent seulement au numérateur mais aucun au dénominateur. Mais si j’étais ingénieur en catalyse, je voudrais comparer ces sphères sur la base de leurs surfaces parce que les surfaces élevées offrent plus de réactivité catalytique. 

La surface de la sphère est Donc pour comparer sur la base de la surface, nous devons trouver le carré des diamètres divisés par le nombre de particules. Puis prendre la racine carrée pour retourner au diamètre moyen. 

C’est encore appelé une moyenne numérique (moyenne surfacique en termes de numération). Le dénominateur dans l’équation est le nombre de particules. On additionne les carrés des diamètres. C’est pourquoi en termes mathématiques, on l’appelle D[2,0] – l’exponent du numérateur est carré et le terme de diamètre est au dénominateur. Si j’étais un chimiste, je voudrais comparer les sphères sur la base de leur poids. L’équation pour le poids d’une sphère est: 

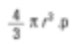
Ensuite, il doit y avoir un nombre de termes d’échelle divisés par le nombre de particules et pour revenir au diamètre moyen, on prend la racine cube.