A key parameter of colloidal systems is their particle size. Yet there are many different methods by which a particle size can be obtained. So which one should be chosen? Comparing stated dimensions from one method with those from another can be confusing and should be approached with caution. In addition to different methods, it is possible to express the same numbers in different ways. Distributions calculated in terms of volume, number or scattering intensity often produce vastly differing results in terms of their mean values and the appearance of the distributions - despite expressing exactly the same physical characteristics of a sample.
The differences between these three distributions are highlighted using a titanium dioxide sample as an example.
Many things in nature have characteristics that show variations. A distribution is a description of the probability of encountering a certain value of a variable. For example, an age distribution of a group of people might express the number of members of that group in each age category. This type of distribution would correctly be denoted as an 'age distribution by number'. When particle size distributions are of interest, three types of distributions are commonly encountered.
The number distribution shows the number of particles in the different size bins. The volumedistribution shows the total volume of particles in the different size bins. The intensity distribution describes how much light is scattered by the particles in the different size bins. Are these three distributions different? Yes they are!
As a simple example, consider a distribution consisting of just two particles, particle species one with size a and particle species two of size b. If there are Na particles with the size a and Nb particles with size b then in terms of number, their relative contributions compared to the other particle are
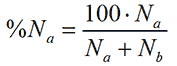 (1)
(1) |
where %Na is the relative number of the particle with size a. Assuming that the particles are spherical, the particle volume is proportional to the size to the third power. Thus, in terms of volume, the relative contribution from a is
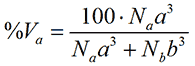 (2)
(2) |
where %Va is the relative volume of the particle with size a. Finally, for small, isotropic particles the scattering intensity from a spherical particle is proportional to the size to the sixth power. Thus, in terms of intensity, the relative contribution from a is
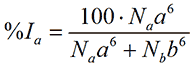 (3)
(3) |
where %Ia is the relative amount of intensity of the particle with size a.
For real-life distributions, the situation can be modeled in a similar way to the simplified two-particle model employed above as an example.
In effect, this typically means that intensity distributions emphasize the larger particles in the distribution, whereas the number distributions emphasize the smaller particles in the distribution. However, it is important to note that both are just different representations of the same physical reality of a distribution of different sizes.
For particles that are much smaller than the wavelength of the illuminating light (typically 632.8nm in the Zetasizer Nano), the above isotropic assumption holds true. A complete description of the more complicated scattering behavior involves the application of Mie scattering. This theory describes how much light is scattered by a particle of any size when the complete optical properties (refractive index and absorption) are known.
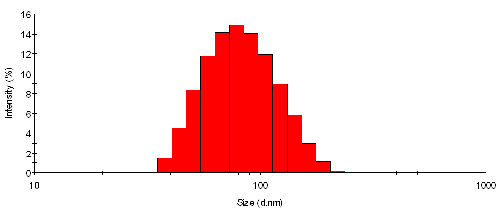
The intensity size distribution from TiO2 particles in water is shown in figure 1. In order to point out the discrete nature of the analysis used, the histogram (steps) rather than the frequency curve (smooth) representation is displayed. The mean size is 87nm with a standard deviation of 32nm - by intensity. The key size parameters obtained are listed in Table 1.
|
| Mean [nm] | Width [nm] | |
|---|---|---|
| Intensity | 87 | 32 |
| Volume | 65 | 25 |
| Number | 50 | 14 |
The volume size distribution from the sample TiO2 particles in water is shown in figure 2. Here the mechanism as described in equation 4 is used to back-calculate the distribution that explains the measured intensity as seen in figure 1. The shape of the distribution is somewhat different, and appears to be biased towards smaller sizes. The mean size is now 65nm with a standard deviation of 25nm - these values are by volume.

|
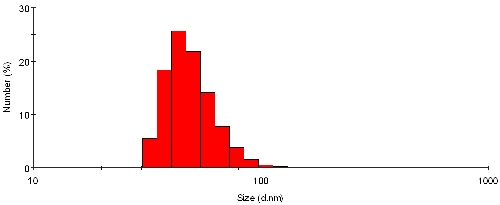
The intensity size distribution from the sample TiO2 may also be transposed into a number distribution, as shown in figure 3. The shape of the distribution is markedly different, and definitely enhances the magnitude of the smaller size bands. The mean size obtained from this representation is 50nm with a standard deviation of 14nm - these values are by number.
|
The easiest answer to this question is that all three are correct. As long as it is clearly stated how the size was obtained and what distribution representation was considered, any of the size distribution provides useful information about the sample.
For practical applications it is worthwhile noting that comparison of different samples should always be done with the same distribution analysis. In other words, two different samples, measured by light scattering, should only be compared by analyzing the same distribution - preferably the intensity as those data are closest to what is really measured, and do not involve any assumptions about the Mie scattering function. For small (<300nm) particles, and those where the parameters for the Mie function are well-known, reliable volume and number distributions can be compared and overlaid, provided the 'raw' data quality is good enough, so that the distribution conversion from intensity to volume and then to number is valid.
When comparing light scattering data with other sizing techniques, the detection mechanism of those technologies must be taken into account. For example, a UV or RI detector coupled to chromatography detects the concentration of material in the eluted phase. Thus, the distribution obtained from such a measurement is effectively a concentration, or in other words a volume or - for the case of a homogeneous population of material of common density - a mass distribution. Consequently, the volume distribution from light scattering would compare best with UV or RI chromatography data.
In (electron) microscopy particles are displayed as numbers in each size bin, i.e. the obtained average size is one which is closest related to the number distribution from light scattering.