粒度分析的基本原理-2

下载



數量分布和體積分布 

 

  上面的例子來自 New Scientist (1991 年 10 月 31 日)。宇宙中有著繞地球軌道運行的物體以及用於確定它們規律性軌道的大量數字。科學家們還基於它們的大小進行了分組。如果我們查看上述第三段，我們便能得出結論，事實上99.3%的粒子極小。這是基於數字的數據。若查看第四段，亦能準確得出幾乎所有物體範圍在10-1000cm之間。這是所有物體的質量。數量和質量的分布截然不同，我們須注意到結論可能會受我們所用的分布影響，而且沒有分布是精確的。數據只是以不同方式檢測。例如，若我們製作太空服，可能會說應注意避免7000的大物體，亦要注意99.96%的情況。然而，對太空服最重要的是以數字保護99.3%小粒子。若計算上表的平均，數平均為約1.6cm，質量平均約為500cm—如此差異巨大。

數量、長度、體積/質量分布的相互轉換

  若用電子顯微鏡測量粒子前述內容（不同技術提供不同平均）可得知D[1,0]或數-長平均大小。如果我們實際需求為質量或體積的平均大小，須將數平均轉為質量平均。數學上, 這很簡單，然而需測試轉換之結果。

 假設電測技術平均大小誤差為+-3%。轉換數平均到質量平均, 時質量平均是直徑的立方函數，那時誤差最終值的立方變為+-27%。

 











  然而，若用激光擴散計算質量或體積分布情況會改變。

  除非解決方案分散法則能在重新循環條件下建立穩定樣品，否則會得到+-0.5%的可重用體積平均。

  若將此體積平均改為數量平均，可能偏差或數量平均為0.5%的平方根且小於1.0%。

  事實上，若用電子顯微鏡實踐體積或質量分布，會意味著忽視或丟失10μduale sẽ相對乎於忽視或丟失1000尺寸1μ的玉米具有相同效果，確認相互轉換具重大風險。

 Malvern 尺寸從 DOS 和 Windows 軟件計算不同直徑，要注意計算，異常數字將以公式（如Hatch-Choate轉換公式-Ref.7）不同方式互相變換。

 

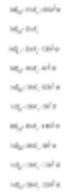
測量及推導直徑

  由 Malvern 激光散射技術的光能量數據分析引發的體積分布分析，可以根據 Fraunhofer 案例面積分布進行假設。這種體積分布可如上所述轉換為任何數字或直徑。

  然而，在技術分析中，我們需要了解這些轉化結果（見前段“數量、長度和體積/質量平均的相互轉換”），此外，應測量並計算平均直徑以測量第一直徑。

  其他技術能從某些已測直徑推導出其他直徑。例如，顯微鏡將測量 D[1,0]及從中獲得其他直徑。

  我們更信賴測量出的直徑，而非求出的直徑。實際上，依賴某些計算出的特性是非常風險的。例如，Malvern 分析表顯示特定表面積(m/cc 或 m/gm)。

  我們不應完全接受該表-若確實需要材料特定表面積，必須使用特定技術如B.E.T或 mercury porosimetry計算表面積。

應使用哪個數值？

  已知其他技術會測量粒子不同特性（或尺寸），我們需要利用許多技術智慧獲得其他平均結果（如D[4,3]，D[3,2]等）。那麼，為何要用數字？

  以1和10units球的直徑為例。假設製造金。若我們計算簡單數平均直徑，按此公式獲得。

 

 

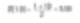
  因此，我們可以假設系統中粒子的平均大小是 5.50 單位。但請記住，如果我們在製作金，我們應該關心重量。

  例如，如果我們知道工藝趨勢，我們不會關心包含350萬粒子的意圖。我們會關心是否有1或2公斤的金。

  記住質量平均是直徑的立方體函數，我們知道直徑為1的球為1質量單位，直徑為10的球為10=1000 質量單位。

  這意味著大球組成系統總質量的1000/1001 部分。若製金，我們可能會丟掉直徑1的球，因為我們只會輸系統總質量的0.1%。因此數平均將顯著偏離生成的質量，D[4.3]可能更有用。

  我們雙球的例子中，質量或體積平均動量將按如下公式計算。

 

 

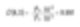
  這數字顯示了系統內的質量分布，對化學工程師而言是有價值的。

  然而，假設在無塵室中製造矽或砷化鎵晶圓片。若有粒子落在晶圓片上，可能導致缺陷。在這一實例中，粒子的數量和濃度非常重要。因為1粒子即1缺陷，我們希望使用能夠直接測量特定數量或粒子濃度的技術。本質上，粒子數量和粒子大小是不同的。總數很重要，我們記錄並計算每個粒子。大小不太重要。我們只需量輪界限中大型檢測規模(如 8中)。從尺寸上看，確定粒子的大小對粒子的尺寸分布貢獻程度不重要，我們需要更多大小帶。

  測量每次吸氣量中 I 和顆粒尺寸貢獻對氣喘病人的重要性。

平均、中位數、眾數 – 基本統計 

 

平均值(Mean)

  這是數據的某種算術平均。可計算粒子數的幾種平均值。(參見D[4,3]部分等)

中位數(Median)

  這是精確將群體分為兩個相等部分的粒子大小值。例如，表示高於和低於該值分布各50%。 

眾數(Mode)

  頻率曲線最高點為最常見值。若假設分布為正態或高斯分佈，平均值、中位數和眾數將位於圖形上相同位置（見圖4）。但若此分佈為雙峰分佈（雙模），見圖5。

 

 

  平均直徑將坐落於如圖所示幾乎兩個分佈之間標準。實際上沒有這樣的平均直徑大小的粒子。中位數直徑約位於兩分布頂80%，因其將兩分布精確分開。最多數值於大分布處，因其為最常見直徑值。



  這實例展示了平均值、中位數、眾數由分布是否對稱決定，沒有理由期望它們完全相同。

這篇文章可能已自動翻譯