顆粒分析的基本原理-1
顆粒分析的基本原理
什麼是顆粒?
這個問題聽起來很愚蠢。但是對於各種顆粒大小的分析技術來說,這是一個基礎。分散過程和材料的形狀使得顆粒大小的分析變得比最初更加複雜。

顆粒大小問題
想像有人給你一個火柴盒,讓你估算它的尺寸是多少。你可能會回答這個火柴盒的尺寸是20*10*5mm。你不會確切地說“火柴盒的尺寸是20mm”,這只是你判斷的一種方式。因此很明顯,用一個單一尺寸去描述三維物體是不可行的。對於像沙粒或油漆中的顏料顆粒這樣的複雜形狀,情況尤其如此。如果我是Q.A.(質量管理)經理,我會希望只用一個數字來描述顆粒 – 例如,我希望知道最近生產的產品平均尺寸是變大還是變小了。這就是顆粒大小分析的基本問題之一 – 我們如何用一個數字來表達三維物體?
等效球體(Equivalent spheres)
有一個可以用單一數字表達的球體。如果我們說一個球體的直徑是50μm,那麼這是精確的。當我們描述一個50μm立方體的邊和對角線時,就會無法精確表示。擁有許多特徵的物體可以通過一個數字來表達。比如與體積和表面積相關的重量是一個確定的數字。如果有技術可以測量火柴盒的重量,那麼我們可以將其轉換為球體的重量。
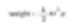
記住,計算與火柴盒相同重量的球的直徑這個數字是一個確定的數字(2r)。這就是等效球體理論。測量任何顆粒的屬性,並想像我們提到的顆粒是球體。因此,我們以一個確定的數字(球的直徑)來表達顆粒。
這告訴我們即使在表達三維物體時,為了控制目的可能會不精確,但我們不需要用3個或多個數字來表達。
這我們也可以看到依賴於物體形狀的有趣效果,並示範一個像球體一樣的圓柱。

但如果圓柱的形狀或尺寸改變,體積/重量也會改變。作為等效球形模型,我們至少可以說它變得更小或更大。
100 x 20μm 圓柱的等效球體直徑
假設圓柱直徑為D1=20μm,高度100μm。這裡有一個與體積相同的D2直徑的球。我们可以像下面這樣計算直徑。
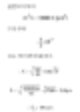
具有100μm高度和20μm直徑的圓柱的球形直徑體積大約是40μm。下面的表格顯示了不同比例的圓柱的球形直徑。最後一行是典型的盤狀大粘土顆粒。由於其高度20μm而厚度為0.2μm,通常不考慮其維度。關於測量顆粒體積的工具,我們大概能在5μm左右獲得答案。因此,可能使用其他技術來質疑這些答案。
此外,這些圓柱可以與例如25μm的過濾器相同大小,並且可以說“所有的物質都小於25μm”。這些圓柱具有不同的值,因為當在激光衍射下顯示時,會有所不同。

各種測量技術
很明顯,如果我們透過顯微鏡觀察顆粒,可以看到它的二維投影,並能測量顆粒的直徑。如果我們接受顆粒的最大長度並將其作為我們的尺寸使用,我們可以說這個顆粒是個最大維度的球顆粒。同樣地,如果我們使用像Feter’s 直徑這樣的最小直徑,我們將得到顆粒大小的另一個答案。因此我們應知道,每種技術可以測量的顆粒的不同物性(最大長度、最小長度、體積、表面積等)。所以如果選擇性測量,它會顯示與其他測量技術不同的結果。

圖3顯示了幾種可以用來描述一顆沙粒的解決方案。每種技術都沒有錯 – 它們都是正確的,測量的是顆粒的不同性質。這就像是用厘米或英寸的方法測量火柴盒(你測量長度而我測量寬度!)。
如此,我們只能通過同樣的技術測量顆粒以便進行比較。這意味著像沙粒這樣的顆粒沒有能做為標準的大小。標準必須通過不同技術的比較來實現。然而,透過每種技術,我們可以獲得標準顆粒大小,這將用於各種設備的比較。
D[4,3]等
設有直徑為1、2、3的3個球體。3個顆粒的平均大小是多少?開始時我們可能會說是2。如何得到這個答案?我們將所有的值相加,然後除以總顆粒數。
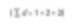
這是數量平均(更準確的說,是長度平均)。顆粒的數量可以用公式來表示。

在數學術語中稱為D[1,0]。原因是在上面的公式中,直徑項(d1)較多,在底下的公式中直徑項(d0)不存在。但如果我是一名與催化劑有關的工程師,我會希望基於表面積來比較這些球體。原因是更高的表面積會帶來更高的催化活性。球體的面積是4πr²。因此,基於表面積來比較時,必須是所有直徑的平方之和除以顆粒數,然後為了回到平均直徑,我們必須計算平方根。

這也是平均(表面數的平均)。因為顆粒的數目出現在下面的公式中,所以我們將所有直徑的平方相加。因此在數學術語上被稱為D[2,0]。因為公式中的上式項是平方而底部是直徑項。如果我是化學專業的,我會希望比較基本重量的球。球的重量表達式為:
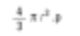
我們需要知道直徑的立方根,然後用其顆粒數目除以結果,以回到平均直徑。

這是再次的數量平均(數-體積或數-重量平均)。因為顆粒的數目出現在公式中。因此在數學術語中它可以表示為D[3,0]。
D[1,0],D[2,0],D[3,0]簡單平均的問題在於顆粒數在公式中是固有的。這需要很多顆粒去計算。計算的顆粒數一般只有在低數(ppm或ppb)時實際上可行,例如污染、控制、清潔等。若每個1g矽的尺寸(密度2.5)均為1μm,則大約有760*10⁹顆粒的簡單計算。
因此必須用瞬時均值的概念來補充,這可能會引起混亂。以下是兩個重要的平均值:
-
D[3,2] – 表面平均 – 塞特平均直徑
-
D[4,3] – 體積或質量平均 – 德布魯克平均直徑
這些平均類似於慣性或其他與直徑相關的線性條款。(如下所示,表面積與d³相關,而體積與質量與d⁴相關。)
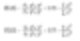
這些公式表示頻率(表面積或體積/質量)分佈的中心點旋轉。實際上,這些是分佈的質心。這種計算方式的優點顯而易見 – 公式中不包含顆粒數,因此運算平均和分佈不需複雜的顆粒數知識。激光衍射起初基於體積參數來計算貢獻,由於這一點,D[4,3]作為重要指標被報告。
測量技術不同測量結果也不同
如果我們使用帶有網絡的電子顯微鏡來測量直徑,以獲得平均值的顆粒數來計算或全部相加。我們可以通過不同的測量方法來獲得不同大小的顆粒。以下是這些技術的簡要介紹:
這篇文章可能已自動翻譯
{{ product.product_name }}
{{ product.product_strapline }}
{{ product.product_lede }}
