100 years ago Gustav Mie developed an analytical solution for Maxwell equations to describe light scattering by spherical particles. One of the most important industrial applications of his model is in laser diffraction particle size analysis.
One hundred years ago Gustav Mie developed an analytical solution for the equations derived by Maxwell to describe the scattering of light by spherical particles. The resulting Mie theory has various uses, one of the most important industrial applications being laser diffraction particle size analysis. Laser diffraction is a well-established particle sizing technique, widely used across a range of manufacturing sectors for the measurement of many different materials. With this method, an optical model unlocks the diffraction pattern produced as light is transmitted through a sample, generating particle size information. Measurement accuracy and range is directly dependent on the model selected. As Mie theory celebrates its centenary it is timely to reflect on its role in the application of laser diffraction particle size analysis and the benefits it brings.
|
Light transmitted through a wet or dry suspension is scattered by the particles in it. Generally speaking, smaller particles scatter light at relatively low intensities to wide angles while larger particles scatter light more strongly at narrow angles. Laser diffraction analyzers capture the diffraction pattern produced by this scattering and then use an optical model to derive the size distribution of the particles that produced it.
Mie theory is based on Maxwell's electromagnetic field equations and predicts the scattering intensity induced by all particles within the measurement range, whether they are transparent or opaque. It is based on the following assumptions:
Mie theory uses the refractive index difference between the particle and the dispersing medium to predict the intensity of the scattered light. It also describes how the absorption characteristics of the particle affect the amount of light which is transmitted through the particle and either absorbed or refracted. This capability to account for the impact of light refraction within the particle is especially important for particles of less than 50µm in diameter and/or those that are transparent.
In the late 1970's, when laser diffraction systems were first introduced, limited computing power made it difficult, and impractical, to rigorously apply Mie theory. The Fraunhofer approximation of the Mie theory was a much easier model to use and was therefore widely adopted at this stage. It provides a simpler approach by additionally assuming that:
These approximations hold for large particles (>50µm) but increasingly they break down as particle size decreases. Fraunhofer is particularly inaccurate below 2µm and also fails to properly characterize systems containing transparent particles. When the refractive index difference between the particles and the surrounding medium is low, inaccuracies also tend to increase.
An important point to recognise is that Fraunhofer may inaccurately predict the size of particles or the amount of material within a given size range, or both. The nature and extent of any inaccuracies is not predictable. Accurate characterization of the overall particle size distribution demands precise determination of both the size and quantity of material present.
The later development of more powerful computers eliminated any need for compromise, enabling application of the more rigorous and comprehensive Mie theory in its entirety. In very many cases this resulted in much improved measurement accuracy. However, the simplicity of Fraunhofer remains a major attraction, particularly the fact that refractive index data are not required.
Today, both models are in use but the ISO standard for laser diffraction particle size analysis, ISO13320, recognises the fundamental superiority of Mie. Mie theory is recommended for analysis across the complete measurement range (0.1 to 3000 µm) while the use of Fraunhofer is limited to systems containing particles that are 50µm or more in size. Instruments that routinely measure particles smaller than this should therefore now support Mie.
Modern analyzers, such as the Mastersizer 2000 from Malvern Instruments, make it easier to access the accuracy of Mie through the inclusion of an extensive database of refractive indices within the software. Long term improvements to the user interface have also enhanced the transparency of the calculation process, demystifying application of the theory. The following industrial examples highlight the performance offered by these systems.
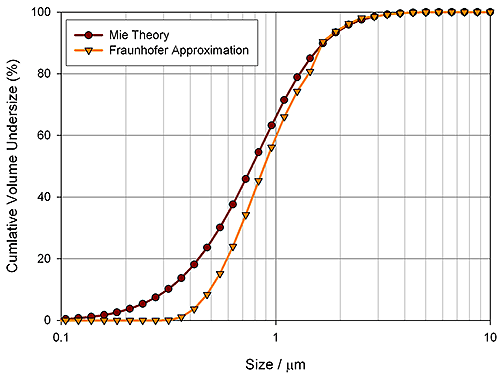
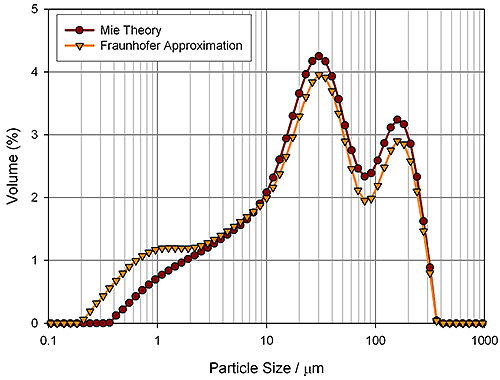
The particle size distribution of calcium carbonate, used as a filler in paper production, is important because within a narrow particle size band there is an increase in optical scattering efficiency that enhances whiteness. Measurements of a calcium carbonate sample made using Mie and Fraunhofer are shown in Figure 2.
Fraunhofer measures the particle size distribution as larger than it is. This error arises from the assumption that the scattering efficiency of particles is the same for all particle sizes. In reality, scattering power decreases rapidly below 0.5µm, so the amount of light scattered from fractions in this size range is very small. When using the Fraunhofer approximation, the scattering observed for these fine particles is assumed to be insignificant, hence the reported volume distribution ends at 0.3µm. Mie Theory, in contrast, predicts the changes in scattering efficiency which occur at small particle sizes, and therefore correctly interprets the low intensity scattering observed from particles in this range as being from a significant volume of particles. This enables the true extent of the distribution to be shown, allowing accurate production control during calcium carbonate milling.
|
The very broad dynamic range accessible through the use of Mie extends the applicability of laser diffraction and is particularly useful when tracking dramatic changes in particle size, such those which occur during milling.
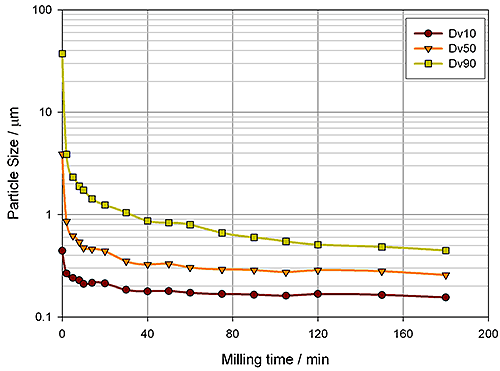
Pigment-based inks for ink jet printers are increasingly common, especially for applications where there is exposure to moisture or a demand for high durability. For these suspensions, wet milling to a particle size of 500 nm or less prevents problems such as blockage of the printer nozzle, defect formation within the printed film and inconsistent colour density. Dispersing the pigment in a suitable mobile phase breaks up lumps and produces a pre-mix which is then milled to a suitable endpoint (see figure 3).
|
These results demonstrate the suitability of Mie-based laser diffraction measurements for monitoring the complete milling process, and identifying the endpoint. After 180 minutes the suspended pigment has a narrow particle size distribution, with a mode of 137nm and a volume median diameter of around 250nm, and should therefore give problem-free operation. Fraunhofer is not suitable for sizing the final product, yielding a median particle size of ca. 800nm instead of 250nm, thereby failing to detect the endpoint.
In the manufacture of refractory products a suspension is either pumped into a mould or coated onto a form with the required shape. Suspensions with high solids loadings are beneficial in terms of finished product strength (post sintering), but may have high viscosity so making handling more problematic. Controlling particle size distribution is one way of optimising suspension properties since increasing polydispersivity allows solid loadings to be raised without increasing viscosity.
|
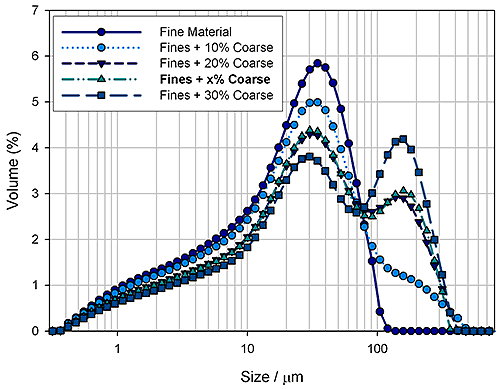
Often manufacturers mix materials with different size distributions in order to control the particle packing density and obtain the desired suspension properties. Figure 4 shows data for samples of refractory materials made of up coarse and fine material fractions. In this study the aim was to determine the amount of coarse fraction in an unknown sample, in order to verify the suitability of laser diffraction for detecting changes in the mixed sample. Using Mie theory, the laser diffraction technique was shown to correctly respond to changes in the mass of coarse particles within the product. The trends observed enable the amount of coarse material within the 'unknown' sample to be identified as 21.6%; this compares with the real figure of 22%. Such accuracy was not possible using the Fraunhofer approximation, because of its inability to account for refraction of light within the particle phase (the particles were transparent in this case). Fraunhofer overestimated the fine fraction (figure 5), leading to an incorrect assessment of the sample mix.
|
Advances in computing power allow modern laser diffraction-based particle analyzers to fully exploit the description of light scattering developed by Mie 100 years ago. The examples included here demonstrate how the ability of Mie theory to correctly predict the effect of particle transparency and changes in scattering efficiency make it superior to the Fraunhofer approximation, particularly for particles less than 50µm in diameter. ISO13320 recognises these benefits, concluding that the Mie theory provides an appropriate optical model across the full laser diffraction measurement range.
Modern measurement systems enable easier access to the powerful capabilities of the Mie theory through the inclusion of, for example, a database of refractive indices. These systems provide the greatest accuracy for the widest possible range of materials.
The Mastersizer 2000 is a laser diffraction-based system from Malvern Instruments that uses Mie theory to provide particle size measurement for many different materials, both wet and dry. It offers a broad measurement range, 0.02µm to 2000µm, and exemplary accuracy of +/- 1%.
Full automation and software-driven Standard Operating Procedures eliminate user variability and streamline analysis, making measurement a simple and routine task. A wide range of 'plug and play' dispersion cassettes ease the switchover from one sample type to another and optimise flexibility.

|