Grundprinzipien der Partikelanalyse-2

Download



Zahlverteilung und Volumenverteilung 

 

  Das obige Beispiel stammt aus der Ausgabe von New Scientist vom 31. Oktober 1991. Es gibt eine große Anzahl von Objekten, deren Umlaufbahn im Weltraum von Menschen für systematische Zwecke definiert wurde, während sie um die Erde kreisen. Wissenschaftler haben außerdem Objekte basierend auf ihrer Größe klassifiziert. Wenn wir den dritten Abschnitt untersuchen, können wir genau ableiten, dass 99,3% aller Partikel unglaublich klein sind, was auf einer datenbasierten Anzahl auswertbar ist. Wenn wir jedoch den vierten Abschnitt untersuchen, können wir genau ableiten, dass praktisch alle Objekte zwischen 10-1000 cm liegen, was der Masse aller Objekte entspricht. Die Verteilung von Anzahl und Masse unterscheidet sich stark, und wir sollten darauf achten, dass die Schlussfolgerungen in Abhängigkeit von der verwendeten Verteilung variieren können. Keine Verteilung ist genau. Daten werden nur anders untersucht. Beispielsweise, wenn wir einen Raumanzug herstellen, könnte man sagen, dass es einfach ist, großen Objekten mit 7000 auszuweichen, und auf 99,96% der Situationen achten muss. Das Wichtigste bei einem Raumanzug ist jedoch der Schutz vor den kleinen Teilchen, die 99,3% der Gesamtanzahl ausmachen. Wenn wir den Durchschnitt der Verteilungen in der oben angegebenen Tabelle berechnen, sollte uns bewusst sein, dass der Zahlendurchschnitt etwa 1,6 cm beträgt und der Massendurchschnitt etwa 500 cm beträgt – diese Veränderungen sind erheblich.

Zahl- und Massendurchschnittsumwandlung

  Wenn Partikel durch ein Elektronenmikroskop gemessen werden, sieht es aus, als ob D[1,0] oder der Zahl-Längen-Durchschnitt berechnet wird (beachten Sie, dass unterschiedliche Techniken unterschiedliche Durchschnitte liefern). Wenn die durchschnittliche Größe der Masse oder des Volumens tatsächlich benötigt wird, muss der Zahlendurchschnitt in einen Massenmittelwert umgewandelt werden. Mathematisch ist dies leicht durchführbar, jedoch müssen die Ergebnisse dieser Umwandlung beurteilt werden.

  Angenommen, elektrische Messtechniken haben eine durchschnittliche Größenabweichung von +-3%. Wenn wir einen Zahlendurchschnitt in einen Massendurchschnitt umwandeln, basierend auf der kubischen Funktion des Durchmessers, wird die Abweichung zum letzten Wert auf das hoch Würfelfach erhöht oder +-27% betragen. 

 











  Wenn jedoch die Masse- oder Volumenverteilung durch Laserstreuung berechnet wird, ändert sich die Situation.

  Unter den Bedingungen der Rezyklierung von Proben unter solider Dispersion lässt sich ein wiederkehrender Volumendurchschnitt von +-0,5% erzeugen.

  Sofern dieser Volumendurchschnitt in einen Zahlendurchschnitt verwandelt wird, wird die Schätzung oder der Zahlendurchschnitt weniger als die dritte Wurzelschätzung des bisherigen Wertes von 0,5% sein oder weniger als 1,0% betragen.

  Tatsächlich bedeutet das, wenn Volumen- oder Massendistribution durch ein Elektronenmikroskop verwendet wird, dass das Übersehen oder der Verlust einer 10μ-Partikelgröße einer entsprechend hohen Zahl von 1μ-Partikeln gleichkommt. Die Gefahr der Verwandlung sollte erkannt werden.

  Die Software von Malvern Sizers sowohl DOS als auch Windows kann unterschiedliche Durchmesser berechnen. Beim Erlangen dieser Durchmesser ist Vorsicht geboten. Unterschiedliche Mittelwerte können aufgebraucht werden, indem die in den nächsten Gleichungen genannten Gleichungen angewendet werden (Hatch-Choate-Verfahrensgleichung- Ref.7).

 

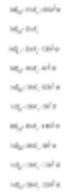
Gemessene und abgeleitete Durchmesser

  Wir haben die Malvern-Laserbeugung als eine Technik gesehen, die eine Volumenverteilung für die Lichtenergiemessung beutet, wie sie durch Fraunhofer-Analysen bestimmt wird. Diese Volumenverteilung kann sogar in eine teilweise gezeigte Zahl oder einen Längendurchmesser umgewandelt werden.

  Bei jeglicher Analysetechnik ist es wichtig, dass diese umgewandelten Ergebnisse bekannt sind, die Umwandlungen von Zahl-, Größen- und Volumen-/Massenmittelwerten im vorherigen Abschnitt abgehandelt werden, und dass der mittlere Durchmesser vom Gerät tatsächlich gemessen und die genauen Änderungen in den ersten gefundenen Durchmesser umgerechnet oder durch diesen berechnet werden.

  Verschiedene Methoden drücken schlussendlich aus, dass andere Techniken von bereits vorhandenen Durchmessern gewonnen werden könnten. Ein Mikroskop misst etwa D[1,0] und dann sind Durchmesserfrequenzen dadurch gewinnbar.

  Gemessene Durchmesser sind erfahrungsgemäß zuverlässiger als abgeleitete Durchmesser. Tatsächlich ist das Verlassen auf eine abgeleitete Charakteristik in realen (hergestellten) Beispielen ein großes Risiko. Der Analysebericht von Malvern gibt erhebliche Daten zu bestimmten Flächen (m/cc oder
m/gm) an.

  Sie sollten sich von einer vollständigen Akzeptanz des Berichts fernhalten. – Es ist besser, spezielle Techniken wie B.E.T. oder Quecksilberporosimetrie zu verwenden, um die speziellen Flächenwerte von Materialien zu errechnen.

Welche Zahl verwenden?

  Andere Techniken, die bereits bekannt sind, messen verschiedene Eigenschaften (oder die Größe) von Partikeln und die Daten müssen durch viele verschiedene Methoden verwendet werden, um andere Durchschnittsergebnisse (D[4,3], D[3,2] etc.) zu erzielen. Warum also sollen wir die Zahl verwenden?

  Betrachten Sie einen einfachen Fall von Durchmessern von 1 und 10 Einheiten. Angenommen, wir stellen Gold her. Wenn wir den einfachen Durchmesserdurchschnitt errechnen, ergibt er sich wie folgt.

 

 

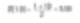
  Demnach könnten wir theoretisch annehmen, dass der Durchmesser der Partikel innerhalb des Systems 5,50 Einheiten beträgt. Denken Sie daran, dass beim Goldherstellungsprozess eine gewisse Aufmerksamkeit auf das Materialgewicht zu lenken ist.

  Wenn wir beispielsweise den Prozess überprüfen müssen, ist die genaue Anzahl der Partikel (350 Millionen) nicht von Interesse. Wir haben eher ein Interesse daran, dass 1 kg oder 2 kg charakteristisches Gold vorhanden sein könnte.

  Da der Massendurchschnitt als kubische Funktion des Durchmessers dargestellt wird, ergibt sich, dass eine Kugel mit 1 Einheit Durchmesser eine Masse von 1 Einheit hat, während eine Kugel mit 10 Einheiten Durchmesser eine Masse von 10^3 = 1000 Einheiten hat.

  Die größere Kugel trägt demnach zu 1000/1001 des totalen Systemgewichts bei. Wenn wir Gold herstellen, könnten wir die Kugel mit 1 einziger Einheit verwerfen, ohne mehr als 0,1% des systemischen Gesamtgewichts zu verlieren. Der Zahlendurchschnitt hätte sich aus dem System in der Tat bedingt. Dies erklärt, warum D[4.3] nützlicher ist.

  Die Bedingungen von Masse sowie Volumen-Mittelmoment würden in unserer Zwei-Kugel-Beispielberechnung so wie folgt aussehen:

 

 

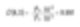
  Diese Zahlen zeigen uns die Verteilung der Gesamtmasse innerhalb des Systems, was für Verfahrenstechniker nützlich ist.

  Angenommen, wir stellen Silizium- oder Galliumarsenidwafer in einem Reinraum her. In diesem Beispiel kann der Kontakt mit einem einzigen Partikel zu einem Defekt führen.

Durchschnitt, Median, Mode – Grundstatistik 

 

Durchschnitt (Mean)

  Ein einfacher arithmetischer Durchschnitt der Daten. Es gibt viele Arten von Durchschnitten, die für die Partikelzählung dienen können (siehe Abschnitte D[4,3] etc.).

Median

  Der Median repräsentiert den Partikeldurchmesser, der die Population in zwei Hälften teilt – 50% liegen über diesem Wert und 50% darunter.

Mode (Modalwert)

  Der häufigste Wert in einer Verteilung oder die Spitze einer Häufigkeitsverteilungskurve ist der Modalwert. Bei einer Normal- oder Gaußverteilung repräsentieren Mean, Median und Mode denselben Punkt. Sehen Sie sich Abbildung 4 an. Bei einer zweimodalen Verteilung wie in Abbildung 5 verteilt sich die Mode um zwei Spitzen.

 

 

  Der Mittelwert in einer bimodalen Verteilung liegt zwischen beiden Peaks, jedoch stellt er keine existierende Partikelgröße dar. Der Medianwert wird in Richtung der stärkeren der beiden Verteilungen um 1% gewichtet sein, da an diesem Punkt die Verteilung genau halbiert. Der Mode ist die Spitze der dominierenden Verteilung, da er den häufigsten Wert des Durchmessers repräsentiert.



  Ein statistisch ideales Beispiel für Mittelwert, Medianwert und Modalwert, das von Verteilungssymmetrien beeinflusst, variiert oder sogar gleichbleiben kann.