Grundprinzipien der Korngrößenanalyse-1

Download



Grundprinzipien der Korngrößenanalyse 

Was ist ein Teilchen?

  Diese Frage zu stellen ist ziemlich naiv. Doch bei den verschiedenen Techniken zur Korngrößenanalyse bilden sie die Grundlage. Der Prozess der Dispersion und die Form des Materials werden bei der Korngrößenanalyse komplexer als zu Beginn.

Partikelgrößenproblem

  Stellen Sie sich vor, jemand gibt Ihnen eine Streichholzschachtel und bittet Sie, die Größe dieser Schachtel zu bestimmen. Vielleicht antworten Sie: 20*10*5 mm. Sie könnten nicht korrekt antworten: „Die Größe der Schachtel ist 20 mm.“, und dies wäre nur eine Ansicht zur Bestimmung der Größe. Man kann die dreidimensionale Natur der Schachtel nicht mit einer einzigen Zahl beschreiben. Offensichtlich wird dies bei komplexeren Formen wie Sandpartikeln oder Pigmentpartikeln in Farbdosen noch schwieriger. Als Qualitätsmanager möchte ich eine Zahl, um die Partikel zu beschreiben – zum Beispiel möchte ich wissen, ob die durchschnittliche Größe des zuletzt hergestellten Produkts zu- oder abgenommen hat. Dies ist ein grundlegendes Problem bei der Korngrößenanalyse. Wie drückt man einen dreidimensionalen Gegenstand mit nur einer Zahl aus?

Äquivalente Kugeln

  Es gibt Kugeln, die mit einer einzelnen Zahl ausgedrückt werden können. Wenn man von einer Kugel mit einem Durchmesser von 50 μm spricht, kann dies genau ausgedrückt werden. Eine Kreide mit einer Kantenlänge von 50 μm kann nicht durch ihre Diagonale und Kantenlänge beschrieben werden. Eine Zahl kann auf die voluminöseste Box angewendet werden. Zum Beispiel ist das spezifische Gewicht des Volumens und der Oberfläche eine bestimmte Zahl. Wenn es eine Technik gibt, das Gewicht einer Streichholzschachtel zu messen, könnten wir dieses Gewicht auf das Gewicht einer Kugel umrechnen.

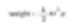
  Wir berechnen das spezifische (2r) für den Durchmesser der Kugel mit dem gleichen Gewicht wie die Streichholzschachtel. Dies ist die Theorie der äquivalenten Kugeln. Wir messen eine Eigenschaft der Partikel und nehmen an, dass die beschriebenen Partikel Kugeln sind. So bekommen wir eine spezifische Größe (Durchmesser der Kugeln) zur Darstellung der Partikel.

   Dies sagt uns, dass wir zwar nicht so genau sein müssen, dass wir die Form mit 3 oder mehr Zahlen ausdrücken müssen, wenn wir einen dreidimensionalen Partikel beschreiben, sondern dass dies für Kontrollzwecke vorteilhaft sein könnte.

   Wir können interessante Effekte erkennen, die von der Form eines Körpers abhängen, und sie mit einem fragilen Zylinder veranschaulicht haben.

  Wenn die Form oder Größe des Zylinders verändert wird, ändert sich das Volumen und/oder Gewicht. Bei einem äquivalenten sphärischen Modell können wir zumindest sagen, ob es kleiner oder größer wurde.

Äquivalenter (sphärischer) Durchmesser eines 100 x 20 μm Zylinders

  Betrachten Sie einen Zylinder mit einem Durchmesser D1=20 μm und einer Höhe von 100 μm. Es gibt eine Kugel mit dem gleichen Volumen wie dieser Zylinder. Wir können den Durchmesser wie folgt berechnen.

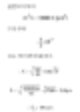
  Das Volumen des kugelförmigen Durchmessers eines Zylinders mit einer Höhe von 100 μm und einem Durchmesser von 20 μm beträgt etwa 40 μm. Die nachstehend aufgeführte Tabelle zeigt die kugelförmigen Durchmesser von Zylindern mit verschiedenen Verhältnissen. Die letzte Zeile könnte ein typisches Plättchen grober Lehm sein, da es eine Dicke von 0,2 μm bei einer Höhe von 20 μm hat und üblicherweise nicht vollständig berücksichtigt werden kann. Bei einem Partikelvolumenmessgerät könnten wir etwa 5 μm als Antwort erhalten. Diese Antwort kann in Frage gestellt werden, indem alternativen Techniken verwendet werden.

  Diese Zylinder können auch in derselben Größe wie ein 25 μm Filter dargestellt werden, und es kann gesagt werden, „alle Material ist kleiner als 25 μm“. Da diese Zylinder unterschiedliche Werte aufweisen, können sie bei der Laserbeugung anders dargestellt werden.

Messen durch verschiedene Techniken

  Offensichtlich, wenn wir Partikel unter einem Mikroskop betrachten, sehen wir sie zweidimensional projiziert, und es gibt den charakteristischen Durchmesser eines Partikels, der dazu geeignet ist, gemessen zu werden. Wenn wir die maximale Länge eines Partikels nehmen und diese als unsere Größe verwenden, können wir sagen, dass das Partikel tatsächlich eine Kugel mit maximaler Dimension hat. Ebenso, wenn wir den minimalen Durchmesser oder einfach den Durchmesser von Feter nehmen, würde das auch eine andere Antwort auf die Partikelgröße geben. Da jede Technik verschiedene Eigenschaften des Partikels wie maximale Länge, minimale Länge, Volumen, Oberfläche usw. messen kann, könnten die Ergebnisse variieren, wenn sie mit anderen Techniken verglichen werden, die selektiv messen.

  Fig 3 zeigt einige mögliche Antworten auf die Beschreibung eines Sandkorns. Jeder Ansatz ist nicht falsch – sie sind alle genau und messen verschiedene Eigenschaften des Partikels. Es ist wie das Messen einer Streichholzschachtel in cm oder inch (Sie messen die Länge, und ich die Breite!).

  So sind wir verpflichtet, durch den Vergleich der gleichen Methode in Pulverform zu messen. Das bedeutet, dass Partikel wie Sandkörner, die Standardgröße, nichts bestimmen können. Standards sollten in der Form sein, die durch den Vergleich von Techniken erhalten werden. Allerdings können wir mit jeder Technik eine Standardpartikelgröße erreichen, wodurch der Vergleich von Geräten ermöglicht wird, die diese Technik verwenden.

D[4,3]etc

  Stellen Sie sich drei Kugeln mit den Durchmessern 1, 2 und 3 Einheiten vor. Wie wäre der mittlere Durchmesser der drei Kugeln? Wir würden annehmen, dass es ungefähr 2 ist. Aber wie erhalten wir diese Antwort? Wir summieren einfach alle Werte und teilen durch die Anzahl der Partikel.

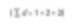
 Dies ist der zahlenmäßige Mittelwert (genauer gesagt der numerische Mittelwert der Längen). Die Anzahl der Partikel kann als Gleichung ausgedrückt werden.

  In mathematischen Begriffen wird dies als D[1,0] bezeichnet. Warum? Weil D1 viele Anzahl im finalen Wert hat und D0 im Nenner steht. Aber wenn ich ein katalytischer Ingenieur wäre, dann würde ich gerne vergleichen, was auf Oberflächenbereich basiert. Das mehr Oberflächenbereich bedeutet höhere katalytische Reaktivität. Die Fläche wird als 4πr2 bestimmt. Daher bei Vergleichen auf dieser Basis müssen wir die Summe des Durchmessers dividieren und dann als durchschnittlichen Durchmesser mit Quadrat auflösen.

  Dies ist ebenfalls der Schwerpunkt-Oberflächen-Mittelwert (oberflächenmittelwert). Warum? Die Teilchenanzahl steht im Nenner. Wir summieren auch alle Durchmesserquadrate. Es wird deshalb D[2,0] genannt. – Weil wir das Quadrat sumieren und der Nenner auf den Durchmesser bezogen ist. Wenn ich Chemiker wäre, würde ich vergleichen wollen, was auf Basis des Grundgewichts ist. Die Formel für das Gewicht einer Kugel ist…

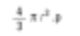
  Es wird auf der Anzahl der Gesamtteilchen dividiert, und wir nehmen die Quadratwurzel dessen, was im Durchschnitt verwendet wird.

  Dies ist wieder ein numerischer Durchschnitt (nummerische Volumen- oder Gewichts-Mittelwert). Weil die Gesamtzahl der Partikel im Nenner vorkommt, wird dies mathematisch als D[3,0] bezeichnet.

  Ein einfaches Mittelwertproblem wie bei D[1,0], D[2,0], D[3,0] bezieht die Anzahl der Partikel in die Darstellung ein. Dies bringt Probleme mit sich, wenn man sehr viele Partikel wie Umweltverschmutzung berechnen muss, typischerweise in geringen Zahlen (ppm oder ppb). Bei 1g Silica (Dichte 2,5), bei einer Größe von 1 μm, wären da etwa 760*109 Partikel, durch eine einfache Berechnung ermittelt.

Daher sind Mitschwingmittel zur Umrechnung vorteilhaft und können Verwirrung verursachen. Zwei wichtige Numerisch sind wie folgt:

• D[3,2]- Flächenmittelwert – Sauter-Durchmesser
• D[4,3]- Volumen- oder Gewichtsmittelwert – De Brouckere-Durchmesser

  Diese Mittelwerte sind wie das Trägheitsmoment und führen eine andere lineare Größe für den Durchmesser ein (wobei Flächen mit d3 und Volumen/Masse mit d4 korreliert).

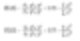
  Diese Formeln zeigen die zentrale Zirkulation der Häufigkeitsverteilung (Flächen oder Volumen/Gewicht). Tatsächlich ist jedes der größte Gewichtspunkt in der Verteilung. Der Vorteil dieser Methode ist klar – die Gleichungen enthalten nicht die Anzahl der Partikel, sodass die Berechnung und Distribution keine komplexe Kenntnis der Partikelanzahl erfordert. Laserbeugung berechnet dabei primär auf dem Volumeneinfluss, daher sehen wir D[4,3] in den Methoden.

Unterschiedliche Messtechniken, unterschiedliche Ergebnisse

  Wenn wir eine Partikelgröße messen wollen und dazu ein Rasterelektronenmikroskop verwenden, um mit den eingelegten Metalllinien zu beobachten, erhalten wir den Durchschnitt, indem wir die Anzahl der Partikel summieren. Wir summieren auch…