Verständnis von Laser-Partikelgrößenanalysatoren und Prinzipien der Partikelgrößenanalyse

Grundprinzipien der Partikelgrößenanalyse

Was sind Partikel?

Dies zu fragen mag eine alberne Frage sein. Aber bei verschiedenen Partikelgrößenanalyseverfahren ist dies von grundlegender Bedeutung. Der Dispersionsprozess und die Form des Materials werden komplexer als bei der anfänglichen Partikelgrößenanalyse.

Problem der Partikelgröße

Angenommen, jemand gibt Ihnen eine Streichholzschachtel und fragt, wie groß sie ist. 

Sie würden wahrscheinlich antworten, dass die Streichholzschachtel die Maße 20*10*5 mm hat. 

Man kann die genaue Größe der Schachtel nicht als 20 mm angeben, was nur eine Perspektive ist. Eine dreidimensionale Streichholzschachtel lässt sich nicht durch eine einzige charakteristische Größe beschreiben.  

Natürlich wird die Situation bei komplexeren Formen, wie den Sandpartikeln oder Pigmentpartikeln in einer Farbdose, noch schwieriger. 

Wenn ich QA (Qualitätssicherungs) Manager wäre, würde ich wünschen, dass Partikel mit einer einzigen Zahl beschrieben werden – um zu wissen, ob die durchschnittliche Größe des zuletzt produzierten Produkts zu- oder abnimmt. Dies ist das grundlegende Problem der Partikelgrößenanalyse: Wie schaffen wir es, einen dreidimensionalen Gegenstand mit nur einer Zahl zu beschreiben? 

 
Abbildung 1 zeigt einige Sandpartikel, aber welche Größe haben sie? 

Äquivalente Kugeln (Equivalent spheres) 

Es gibt eine Kugel, die durch eine einzigartige Zahl beschrieben werden kann. Wenn wir über eine Kugel mit einem 50μm Durchmesser sprechen, dann ist dies exakt darstellbar. Beim Sprechen über einen 50μm-Würfel kann man die Kanten und Diagonalen nicht eindeutig beschreiben. 

Viele Eigenschaften eines Streichholzschachtel-ähnlichen Objekts können durch eine einzige Zahl beschrieben werden. Beispielsweise ist Gewicht in Bezug auf Volumen und Oberfläche eine spezifische Zahl. Wenn wir die Technologie hätten, das Gewicht einer Streichholzschachtel zu messen, könnten wir es in das Gewicht einer Kugel umrechnen. 

Denken Sie daran, 

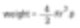
und berechnen einen spezifischen Wert (2r) für den Durchmesser einer Kugel mit demselben Gewicht wie die Streichholzschachtel. Dies ist die Theorie der äquivalenten Kugel. 

Wir messen die Eigenschaften eines Partikels und beziehen uns dabei auf ein als Kugel angenommenes Partikel. Wir erhalten somit eine spezifische Zahl (Durchmesser der Kugel) zur Darstellung des Partikels. 

Dies bedeutet, dass, obgleich es unpraktisch sein mag, für Kontrollzwecke mehr als eine Zahl zur Darstellung eines dreidimensionalen Partikels zu verwenden, keine Notwendigkeit besteht, mehr als eine oder zwei Zahlen zu verwenden. 

Diese interessante Effektillustration verdeutlicht die Abhängigkeit von Objekten von Form zu Form, wie zum Beispiel bei einem Zylinder, der einer Kugel geähnelt wird. (Abb. 2) 

Sollten sich die Form oder Größe des Zylinders ändern, würde sich das Volumen/Gewicht ändern. Wir könnten im Modell der äquivalenten Kugel zumindest sagen, dass es kleiner oder größer geworden ist. 

Äquivalenter kugelförmiger Durchmesser eines 100 x 20μm Zylinders 

Nehmen wir an, der Durchmesser des Zylinders beträgt D1=20μm und die Höhe 100μm. Es gibt eine Kugel mit einem Durchmesser D2, die dem gleichen Volumen wie der Zylinder entspricht. Wir können den Durchmesser wie folgt berechnen: 

Volumen des Zylinders 

Volumen der Kugel 

X ist der Volumenradiuswert. 

Das Volumen des kugelförmigen Durchmessers eines Zylinders mit einer Höhe von 100μm und einem Durchmesser von 20μm beträgt etwa 40μm. Die folgende Tabelle zeigt die kugelförmigen Durchmesser bei verschiedenen Zylinderverhältnissen. Die letzte Zeile könnte ein typischer dickscheibenartiger Tonpartikel sein. Da die Höhe 20μm beträgt und die Dicke 0,2μm, müssen wir die Dimensionen normalerweise nicht berücksichtigen. 

Wenn wir mit einem Instrument messen, das das Volumen des Partikels misst, erhalten wir möglicherweise eine Antwort von etwa 5μm. Daher müssen wir für potenzielle Einwände gegen diese Antwort eine andere Technik verwenden. 

Zudem könnten alle diese Zylinder durch einen Filter von 25μm Größe angezeigt werden, sodass gesagt werden kann „alles ist unter 25μm“. Da jeder dieser Zylinder unterschiedliche Werte hat, könnten sie bei der Laserdiffusion anders erscheinen. 

Verschiedene Messtechniken

Offensichtlich, wenn wir die Partikel durch ein Mikroskop betrachten, sehen wir eine zweidimensionale Projektion, und es gibt bestimmte Partikeldurchmesser, die charakterisiert und gemessen werden können. Wenn wir die maximale Länge des Partikels akzeptieren und sie als unsere Größe verwenden, ist es in Ordnung zu sagen, dass das Partikel ein kugelförmiges Partikel mit maximalen Dimensionen ist. 

In ähnlicherweise, wenn wir den minimalen Durchmesser oder den Feters Durchmesser verwenden, wird dies uns eine andere Antwort über die Größe des Partikels geben. Deshalb sollte man sich der Variationen bewusst sein, die jede Technologie bei der Messung der unterschiedlichen physikalischen Eigenschaften des Partikels zeigen kann (maximale Länge, minimale Länge, Volumen, Oberflächenbereich, etc.). Somit, wenn man selektiv misst, könnte es im Vergleich zu den übrigen Messtechniken unterschiedliche Resultate geben.

Abbildung 3 zeigt einige verschiedene Antworten, die eine Sandpartikelgröße charakterisieren können dasselbe Partikel. Jede Technik ist korrekt – die Techniken sind korrekt und messen unterschiedliche Eigenschaften des Partikels. Es ist wie das Messen einer Streichholzschachtel entweder in cm oder inches (Sie messen die Länge, ich messe die Breite!). 

 
In dieser Weise können wir nur in Gestalt von Vergleichen unter denselben Messtechniken zwischen Pulvern bezüglich Standardgrößen messen. Dies bedeutet, dass es keine Standardgrößenbestimmungen für Partikel wie Sandkörner gibt. Standardeinheiten müssen innerhalb der Messtechnik verglichen werden. Dennoch können wir modifiziert als Teil der genutzten Technik zur Größenbestimmung geltend machen wird, und es wird einen Vergleich der Ausrüstung, die die Technik nutzt, ermöglichen. 

D[4,3]

Nehmen wir an, wir haben drei Kugeln mit Abmessungen von 1,2 und 3 Einheiten. Was wäre die durchschnittliche Größe der drei Partikel? Anfangs könnten wir 2 sagen. Wie bekamen wir diese Antwort? 

Wir würden alle Werte summieren und durch die Anzahl der Partikel teilen.   

Das ist der Zahlenmittelwert (korrekter gesagt ist es der nummerische Mittelwert der Länge). Die Zahl der Partikel kann durch eine Gleichung dargestellt werden.  

In mathematischen Begriffen ist dies als D[1,0] bekannt. Der Grund ist, dass der obige Teil der Gleichung (d1) viele Durchmesser hat, während der untere Teil der Gleichung keinen Durchmesser (d0) hat. Sollte ich ein Chemieingenieur sein, hätte ich den Wunsch, diese Kugeln auf der Grundlage ihres Oberflächenbereichs zu vergleichen, da ein höherer Oberflächenbereich tendenziell eine höhere katalytische Reaktivität aufweist. 

Die Oberfläche einer Kugel beträgt . Um basierend auf der Oberfläche zu vergleichen, müssen wir die Summe der quadrierten Durchmesser nehmen, diese durch die Anzahl der Partikel teilen und anschließend die Quadratwurzel dafür ziehen, um zum durchschnittlichen Durchmesser zurückzukehren. 

Das ist wiederum der Zahlenmittel (der durchschnittliche Oberflächenbereich). Der Grund ist, dass die Anzahl der Partikel im unteren Teil der Gleichung ist. Wir summieren die Quadrate der Durchmesser und daher wird es in mathematischen Begriffen als D[2,0] bezeichnet. – Der obere Teil der Gleichung ist quadriert und der untere Teil ist ohne Durchmesserbegriff. Sollten Sie ein Chemiker sein, werden Sie sicherlich die Basiseinheit der Kugel vergleichen wollen. Die Formel für die Kugelgewichtung lautet wie folgt. 

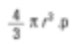
Wir müssen die cubischen Wurzeln von Werten nehmen, die mit dem Gewichtsteil zusammenhängen, indem wir die Summe durch die Anzahl der Partikel teilen und dann die kubische Wurzel daraus extrahieren, um zum durchschnittlichen Durchmesser zurückzukehren.