Principio básico del análisis de partículas-2

Descargar

Distribución de número y volumen 

 

  El ejemplo de arriba es de New Scientist (31 de octubre de 1991). Hay un gran número designado por el hombre para orbitar alrededor de la Tierra en el espacio y sus órbitas regulares. Los científicos también clasificaron grupos en función de su tamaño. Si examinamos el tercer párrafo anterior, inferiremos con precisión que el 99.3% de todas las partículas son increíblemente pequeñas. Esto es una evaluación basada en el número. Sin embargo, si examinamos el cuarto párrafo, inferiremos con precisión que prácticamente todos los objetos tienen entre 10 y 1000 cm. Esta es la masa de todos los objetos. La distribución por número y la distribución por masa son muy diferentes, y debemos notar que nuestras conclusiones pueden diferir dependiendo de la distribución que usemos. Además, ninguna distribución es exactamente correcta. Los datos simplemente se examinan de otras formas. Por ejemplo, si estamos fabricando trajes espaciales, podríamos decir que es fácil evitar 7000 objetos grandes y prestar atención al 99.96% de todos los casos. Sin embargo, lo más importante en un traje espacial es proteger contra el 99.3% de partículas pequeñas determinadas por el número. Si calculamos la media de las distribuciones en la tabla anterior, debemos saber que la media de número es aproximadamente 1.6 cm y la media de masa es aproximadamente 500 cm. – Así de diferentes son.

Conversión mutua de distribuciones numéricas, de longitud, de volumen/mass

  Si medimos las partículas con un microscopio electronico, podemos calcular D[1,0] o el tamaño promedio de longitud-numero a partir del contenido anterior (donde diferentes técnicas ofrecen diferentes promedios). Si realmente queremos el tamaño promedio en masa o volumen, debemos convertir el promedio numérico al promedio de masa. Matemáticamente, esto es fácilmente viable, pero necesitamos verificar el resultado de tal conversión.

Supongamos que la técnica de medición eléctrica tiene un error en el tamaño promedio de ±3%. Cuando cambiamos el tamaño promedio a uno de masa, el error se convierte en el cubo del diámetro, lo que resulta en ±27%.

 











  Sin embargo, si calculamos las distribuciones de masa o volumen a través de la dispersión láser, el escenario cambiará.

  Bajo condiciones de redistribución persistente por dispersión de solución, es posible generar un promedio reutilizable de volumen ±0.5% cuando se mide una muestra estable.

  Si ahora convertimos este promedio de volumen a un promedio de número, la probable desviación del promedio de número será más pequeña que la raíz cúbica de 0.5%, inferior a 1.0%.

  En realidad, si un electrón microscópico se utiliza para observar distribuciones de volumen o masa, ignorar o perder una partícula de 10µ tiene el mismo resultado que ignorar o perder mil de tamaño 1μ. Por ende, debemos ser conscientes del riesgo significativo de conversión cruzada.

  Tanto el software Dos como el de Windows para Malvern Sizers calcularán diferentes diámetros. Sin embargo, prestamos especial atención al encontrar estos diámetros. Diferentes métodos o significados pueden ser así transformados mediante fórmulas, como las variaciones de Hatch-Choate – Ref.7.

 

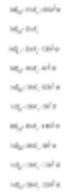
Diámetro derivado y medido

  Hemos observado cómo la tecnología de difracción láser Malvern genera distribuciones de volumen para analizar los datos de energía de luz. (Tenga en cuenta que se supuso una distribución por área, investigada a través del análisis de Fraunhofer.) Como se ha indicado anteriormente, esta distribución del volumen se puede convertir en números o longitudes de diámetro.

  Sin embargo, dentro de cualquier técnica de análisis, necesitamos conocer este resultado convertido (vea la sección anterior sobre «Conversión mutua entre promedios de longitud, número y volumen/masa») y, también, debemos saber si el diámetro promedio está realmente medido por la máquina o calculado a partir del primer diámetro medido.

  Diferentes técnicas podrán obtener otros diámetros ya calculados a partir de diámetros previamente medidos. Por ejemplo, un microscopio puede medir D[1,0] a partir del cual se pueden adquirir otros diámetros.

  Podemos confiar más en los diámetros medidos que en los obtenidos. De hecho, en algunos ejemplos prácticos, depender de características adquiridas (calculadas) puede ser peligroso. Por ejemplo, las tablas de análisis de Malvern nos pueden ofrecer un área superficial específica (m/cc o m/gm).

  No debemos aceptar completamente la tabla. En realidad, si lo que nos interesa verdaderamente es el área superficial específica de un material, debemos usar técnicas especiales que permitan calcular el área de superficie como B.E.T. o porosimetría de mercurio.

¿Qué número usar?

  Otra técnica que conocemos ya mide una propiedad diferente (o tamaño) del partícula y usaremos los datos dentro de muchos otros métodos para obtener otros resultados promedio (D[4,3], D[3,2] etc.). ¿Por qué entonces usar números?

  Consideremos simplemente los diámetros de dos esferas de 1 y 10 unidades como ejemplo. Supongamos que estamos fabricando oro. Si calculamos un diámetro de promedio numérico simple, esto se da tal como sigue.

 

 

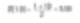
  Por lo tanto, podemos asumir que el tamaño promedio de partículas en el sistema es 5.50 unidades. Sin embargo, debemos recordar que si estamos fabricando oro, deberíamos preocuparnos por el peso del material.

  Por ejemplo, si sabemos la tendencia del proceso, no nos interesarán los 350 millones de partículas allí. Estaremos más interesados en el hecho de que hay 1kg o 2kg de oro.

  Dado que la media de masa es el cubo del diámetro, sabemos que una esfera de 1 unidad tiene una masa de 1 unidad, y una esfera de 10 unidades tiene una masa de 1000 unidades.

  Esto significa que la esfera mayor constituye 1000/1001 partes de la masa total del sistema. Si estamos haciendo oro, podríamos descartar la esfera de 1 unidad, ya que perderíamos menos del 0.1% de la masa total del sistema. Por lo tanto, la media de número puede dar lugar a conclusiones incorrectas sobre la masa derivada del sistema. Es más útil en D[4.3].

  Dentro del ejemplo de las dos esferas, el momento medio de volumen o masa se calcularía como la siguiente fórmula.

 

 

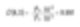
  Esta cifra nos muestra dónde está situada la masa en el sistema, lo cual es un valor significativo para los ingenieros de procesos químicos.

  Pero supongamos que estamos fabricando obleas de silicio o arseniuro de galio en una sala limpia. Si una partícula se deposita sobre la oblea, tendería a causar un defecto. En este ejemplo práctico, el número o la concentración de partículas es muy importante. Dado que una partícula corresponde a un defecto, queremos usar técnicas que midan el conteo específico y la concentración directamente. En esencia, esto es diferente al total de partículas frente al tamaño. Para el total de partículas, registramos y contamos cada una. El tamaño es menos importante. Solo necesitamos la escala del tamaño límite (como se menciona en 8). En términos de tamaño, los números de partículas de tamaño específico están menos relacionados con el tamaño o su contribución general y necesitamos más bandas de tamaño.

  Al medir un inhalador de dosis para pacientes asmáticos, tanto la concentración del fármaco como la contribución del tamaño de partículas son importantes.

Media, mediana, moda – Estadísticas básicas 

 

Media

  Esta es alguna media aritmética de los datos. Existen muchas promedios para calcular partículas (consulte la sección D[4,3] etc.).

Mediana

  Esta es el valor del tamaño de partícula que divide exactamente la población en dos partes iguales. Significa el 50% de los valores por encima y por debajo de este valor. 

Moda

  El valor igual al punto más alto de un gráfico de frecuencias es el valor más común de la distribución de frecuencia. Consideremos esta distribución como Gaussiana. La media, mediana y moda estarán en la misma ubicación. Vea la Fig. 4. Pero consideremos una distribución de dos picos, como la Vista 5.

 

  El diámetro promedio casi exactamente estará entre las dos distribuciones en el gráfico. Tenga en cuenta que tal partícula de tamaño promedio no existe. El diámetro de la mediana estará aproximadamente un 1% hacia el lado mayor de las distribuciones, ya que divide exactamente las dos distribuciones. La moda será el pico de la distribución superior, porque es el valor más común del diámetro.

  Los conceptos de media, mediana y moda centralizados, influenciados por la simetría de la distribución, pueden no ser ideales o incluso coincidir. Este ejemplo explica por qué no tienen que serlo.

Este artículo puede haber sido traducido automáticamente.