Principios básicos del análisis de granulometría-1

Descargar



Principios básicos del análisis de granulometría 

¿Qué es una partícula?

  Preguntar esto es una cuestión muy tonta. Sin embargo, esta es la base en las diversas tecnologías de análisis del tamaño de partículas. El proceso de dispersión y la forma del material se vuelven mucho más complejos en el análisis del tamaño de partículas en comparación con el principio básico.

Problema del tamaño de las partículas

  Supongamos que se le da a alguien una caja de fósforos y le preguntan por su tamaño. Probablemente dirían que mide 20*10*5 mm. No podrían responder con precisión «el tamaño de la caja es de 20 mm», lo cual es una perspectiva al describir el tamaño. No se puede describir una caja de fósforos tridimensional con solo un valor. Claramente, esto se vuelve aún más difícil con formas complejas como las partículas de arena o los pigmentos en una lata de pintura. Como gerente de control de calidad, querría un solo valor para describir una partícula – por ejemplo, saber si el tamaño promedio del producto final está aumentando o disminuyendo. Este es el problema fundamental del análisis de tamaño de partículas. – ¿Cómo podemos representar un objeto tridimensional con un solo número?

Esferas equivalentes

  Existe una esfera que puede representarse con un único número. Si hablamos de una esfera de 50μm, esto puede expresarse con precisión. Sin embargo, no podemos expresar lo mismo cuando hablamos de la esquina o la diagonal de un cubo de 50μm. Una caja de fósforos con muchas características puede representarse con un único número. Por ejemplo, el peso relacionado con el volumen y el área de superficie tiene un valor específico. Entonces, si existe una técnica para medir el peso de la caja de fósforos, podríamos convertir su peso al peso de una esfera. 

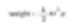
  Recordemos que el diámetro de una esfera con el mismo peso que una caja de fósforos se calcula con un valor específico (2r). Esta es la teoría de la esfera equivalente. Medimos las propiedades de una partícula y asumimos que la partícula mencionada es una esfera. Así, obtenemos un número específico (el diámetro de la esfera) para representar la partícula.

   Esto indica que al representar partículas tridimensionales, aunque puede ser incómodo para algunos propósitos de control, no es necesario expresar con tres o más números.

   Esto permite observar interesantes efectos dependientes de la forma del objeto, y un cilindro puede representarse como una esfera.

  Sin embargo, si cambia la forma o el tamaño del cilindro, el volumen/peso cambiará. Y con el modelo de esfera equivalente, puede decirse, al menos, que es más pequeño o más grande.

Diámetro equivalente de una esfera para un cilindro de 100 x 20μm

  Consideremos un cilindro con un diámetro de D1=20μm y una altura de 100μm. Existe una esfera con un diámetro D2 que es igual en volumen al cilindro. Podemos calcular el diámetro de la siguiente manera.

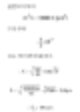
  El volumen del diámetro esférico de un cilindro de 100μm de altura y 20μm de diámetro es aproximadamente 40μm. La tabla de abajo muestra varios valores del diámetro de la esfera para diferentes proporciones de cilindros. La última fila indica una partícula de arcilla grande, típicamente en forma de disco, con una altura de 20μm y un grosor de 0.2μm, que generalmente se considera insignificante en cuanto a dimensiones. Al utilizar un dispositivo de medición de volumen de partículas, podríamos obtener una respuesta en el rango de 5μm. Por lo tanto, debería usarse otra técnica para discutir la posibilidad de tales respuestas.

  Además, todos estos cilindros podrían expresarse como del mismo tamaño que un filtro de 25μm, lo que permitiría decir que «todos son menores de 25μm». Dado que estos cilindros varían en valores, podrían parecer diferentes durante la difracción láser.

Técnicas de medición variadas

  Claramente, si miramos una partícula bajo un microscopio, veremos una proyección bidimensional, y los diámetros característicos de la partícula pueden medirse. Si aceptamos la longitud máxima de la partícula como nuestra medida, podríamos afirmar que la partícula es un esferoide con el máximo tamaño. Igualmente, si usamos magnitudes como el diámetro mínimo o el diámetro de Feter, esto proporcionaría otra respuesta sobre el tamaño de la partícula. Por estas razones, es importante conocer que cada técnica puede medir diferentes propiedades de la partícula (longitud máxima, mínima, volumen, área de superficie, etc.). Por lo tanto, si se elige medir selectivamente, los resultados pueden diferir de otras técnicas.
.

  La Figura 3 muestra algunas respuestas diferentes que podrían definir un único grano de arena. Cada técnica no está equivocada – todas son correctas y miden diferentes propiedades de la partícula. Es como medir una caja de fósforos en centímetros o pulgadas (tú mides la longitud y yo mido el ancho).

  Por lo tanto, solo se pueden comparar al ser medidas como polvo utilizando la misma técnica. Eso significa que para partículas como los granos de arena, no hay un tamaño estandarizado aplicable. Los estándares deben ser esféricos solo para comparaciones entre técnicas. Sin embargo, se puede obtener un tamaño de partícula estándar con cada técnica, permitiendo la comparación de equipos que utilizan la técnica.

D[4,3] etcétera

  Consideremos tres esferas con tamaños 1, 2 y 3. ¿Cuál sería el tamaño promedio de las tres partículas? A primera vista, tal vez digamos que es 2. ¿Cómo obtuvimos esta respuesta? Sumaríamos todos los valores y los dividiríamos por el número total de partículas.
.

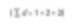
 Este es el promedio aritmético (más precisamente, el promedio de los números basado en longitud). El número de partículas puede expresarse como una ecuación.

  En términos matemáticos, es llamado D[1,0]. La razón es que la parte superior de la ecuación tiene muchos términos de diámetro (d1), mientras la parte inferior no tiene términos de diámetro (d0). Sin embargo, si yo fuera un ingeniero catalítico, desearía comparar estos esferoides basándome en su área de superficie, ya que una mayor área de superficie indica mejor reactividad del catalizador. El área de superficie de una esfera es 4πr2. Por lo tanto, al comparar basándose en el área de superficie, es necesario encontrar los cuadrados de los diámetros y dividirlo por el número de partículas. Y para volver al promedio de diámetro, es necesario tomar la raíz cuadrada de la suma de cuadrados.

  Esto nuevamente es un promedio aritmético (promedio de número de superficie). La razón es que el número de partículas se muestra en la ecuación. Sumamos todos los cuadrados de los diámetros. Matemáticamente, es llamado D[2,0]. – La parte superior de la ecuación es el cuadrado y la parte inferior no tiene término de diámetro. Si fuera un estudiante de química, querría comparar las esferas basándome en el peso. La ecuación del peso de una esfera es la siguiente.

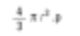
  Debemos encontrar la raíz cúbica del volumen dividido por el número de partículas para regresar al diámetro promedio.

  Esto nuevamente es un promedio aritmético (de volumen o peso promedio). La razón es que el número de partículas es mostrada en la ecuación. Matemáticamente, esto es representado como D[3,0].

  Los problemas con los sencillos promedios de D[1,0], D[2,0], D[3,0] es que el número de partículas es inherente a la fórmula. Esto genera la necesidad de calcular un gran número de partículas. La calculación de partículas es usualmente practicada solo cuando las concentraciones son bajas (ppm o ppb) en aplicaciones como contaminación, control o limpieza. Un cálculo simple indica que la sílice de 1g (densidad 2.5) con todas las partículas de 1μm son aproximadamente 760*109 partículas.

Por lo tanto, el promedio de momento necesita ser suplementado, lo que puede causar confusión. Dos promedios importantes son:

• D[3,2]- Promedio del área – Diámetro promedio de Sauter
• D[4,3]- Promedio de volumen o masa – Diámetro promedio de De Brouckere

  Estos promedios son similares al momento inercial e introducen otro término lineal relacionado con el diámetro. (Donde el área de superficie se correlaciona con d3 y el volumen y la masa con d4).

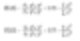
  Estas fórmulas señalan el centro de gravedad que rota en una distribución de frecuencia (de superficie o de volumen/masa). Esencialmente, son el centro de gravedad de cada distribución. La ventaja de este método de cálculo es evidente: la fórmula no incluye el número de partículas, por lo que el cálculo de promedios y distribuciones no requiere del conocimiento del número complicado de partículas. La difracción láser calcula primero la contribución basada en el término de volumen. Y por eso D[4,3] está ampliamente documentado en esta metodologías.

Técnicas de medición distintas resultan en resultados de medición distintos

  Si queremos medir el diámetro de las partículas usando un microscopio electrónico con una rejilla, sumaremos todos los valores y los dividiremos por el número de partículas para obtener el resultado promedio. Esto concluye diciendo que la técnica utilizada tiene.