Notas técnicas sobre reología – Comprensión de la correlación entre la reología y los parámetros de partículas



Descargar



Comprensión de la correlación entre la reología y los parámetros de partículas 

  Las propiedades de los materiales en partículas pequeñas son influenciadas tanto por la distribución de su tamaño como por el potencial zeta (mide la carga de las partículas) sobre la reología del material de recubrimiento. Los resultados de las pruebas han tratado diferentes tipos de recubrimientos para los efectos mencionados, y su reología se midió con el reómetro Malvern Bohlin Gemini.El tamaño de las partículas y el potencial zeta fueron medidos por el Malvern Mastersizer 2000 y el Malvern Zetasizer Nano ZS, respectivamente.

  Los ejemplos usados en este material consideran lo más común en la mayoría de las condiciones y la teoría se puede aplicar ampliamente en los sistemas de recubrimiento.

  La «fluidez» de un material se expresa mediante su viscosidad o resistencia al flujo. Cuando hablamos de la viscosidad de un material específico, es importante entender que no se trata solo de un solo valor, sino que es una función del esfuerzo cortante.

  El esfuerzo cortante es un indicador de la deformación que un material experimenta al ser sometido a esfuerzos cortantes pequeños inferiores a 1s-1 o altos superiores a 100s-1.

  Se resume en la Tabla 1 el proceso para materiales de recubrimiento y los rangos de velocidades de corte correspondientes.

  Pensando en términos de velocidad de corte, los materiales utilizados durante el recubrimiento siguen las siguientes categorías.

– Engrosamiento por corte (fenómeno donde la viscosidad aumenta con la velocidad de corte);
– Newtoniano (fenómeno donde se mantiene una viscosidad constante a través de todas las velocidades de corte);
– Adelgazamiento por corte (fenómeno donde la viscosidad disminuye a medida que aumenta la velocidad de corte);

Relación entre tamaño de partículas y reología

  El primer aspecto a considerar es la viscosidad del PSA (adhesivo sensible a la presión: material que puede adherirse a una superficie (substrato) con presión débil y que presenta adhesividad bajo condiciones de temperatura ambiente). En el caso de partículas de látex, hay dos tamaños diferentes. Como se puede observar en la Fig 1, a medida que aumenta el tamaño de partícula, la viscosidad del PSA disminuye notablemente.

  Esto se debe íntegramente al cambio en el tamaño medio de las partículas. La fracción volumétrica (o la masa de látex añadida al PSA) se mantiene constante. Para una masa de látex dada, el número de partículas dependerá de su tamaño, es decir, habrá más partículas de látex de 175 micrómetros que de 750 micrómetros.

  Esto es una interacción general entre partículas, y en el caso de partículas grandes, la interacción será menor y podría ser una interacción mecánica o electroquímica/química. Por lo tanto, habrá más partículas pequeñas en el mismo volumen, y por ende más interacciones.

  Cuando consideramos la interacción como una estructura estrecha, esencialmente la viscosidad tiende a aumentar. La velocidad de cizallamiento puede ser vista como un factor de deformación, donde velocidades de cizallamiento bajas provocan menores deformaciones que las altas. Por lo tanto, las bajas velocidades de cizallamiento inducen menos deformación que las altas. La Figura 1 también muestra que la mayor diferencia de viscosidad ocurre en velocidades de cizallamiento bajas, ya que las interacciones entre partículas son débiles y se rompen fácilmente.

  Así, ambos sistemas muestran viscosidad similar a altas velocidades de cizallamiento donde las interacciones entre partículas son menos frecuentes.

  En el caso de tintas a base de resina (tintas que usan talco como relleno), la viscosidad dentro del sistema variará. En la Figura 2, la tinta original muestra una viscosidad newtoniana típica. La resina añadida, al ser un material bastante rígido, muestra interacciones moleculares que provocan una viscosidad considerablemente alta, manifestándose como el menor adelgazamiento de cizallamiento debido a que este tipo de enlace polimérico resiste el esfuerzo cortante.

  En el caso de las partículas de talco de 19 micrómetros, siendo las partículas de tamaño relativamente grande, las interacciones son mínimas y la viscosidad inicial muestra una ligera tendencia newtoniana al aumentar. Sin embargo, cuando se incluyen partículas pequeñas de 5 micrómetros, debido al incremento del número de partículas, se observa un aumento notable en la viscosidad. De nuevo, estas interacciones entre partículas son generalmente débiles. Por lo tanto, con el adelgazamiento de cizallamiento, se manifiestan como una viscosidad elevada a velocidades de cizallamiento bajas.

Impacto del volumen y dispersión

  Hasta ahora hemos discutido sobre el relleno con un volumen fijo. Básicamente, se han introducido partículas de tamaño constante en el sistema. Al aumentar simplemente la fracción de partículas, la viscosidad medida por el viscosímetro generalmente aumentaría. Sin embargo, al medir efectivamente la reología, la relación entre viscosidad y velocidad de cizallamiento necesita más información. La Figura 3 muestra que a diferentes velocidades de cizallamiento, la viscosidad de la tinta aumenta con el incremento de la fracción de volumen de partículas, pero también muestra cambios en la fluidez.

  Generalmente, a bajas fracciones de volumen (40% o menos), la cantidad de partículas en el sistema es tan baja que no hay intercambio entre ellas manteniendo así las características newtonianas. Alrededor del 50%, la cantidad de partículas interactuará fuertemente incrementando la viscosidad. Como discutido antes, estas interacciones pueden ser descritas como débiles y al aplicar fuerzas de cizallamiento altas se rompen fácilmente resultando en adelgazamiento por cizallamiento.

  En sistemas con una fracción de volumen superior al 60%, las interacciones serán claramente mayores, manifestándose en viscosidades altas incluso a velocidades de cizallamiento bajas con comportamiento de adelgazamiento por cizallamiento. Sin embargo, se deben considerar las dificultades mecánicas del movimiento de partículas en estos sistemas complejos, que se vuelven más visibles a altas velocidades de cizallamiento y resultan en un aumento de viscosidad. En ese momento, muestran características de engrosamiento por cizallamiento o dilatante.

  La viscosidad dependiente del volumen puede describirse con la ecuación de Krieger-Dougherty. η representa la viscosidad de la suspensión, ηmedium es la viscosidad del medio base, φ es la fracción de volumen de sólidos en la suspensión y φm es el valor máximo de dicha fracción.

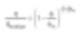
  Además, [η] representa la viscosidad intrínseca del solvente (viscosidad intrínseca) y en el caso de partículas esféricas es 2.5. La ecuación de Krieger-Dougherty puede variar según las propiedades de la partícula, incluso con una fracción de volumen fija. En este caso, se trata del tamaño de partícula o el rango de intervalo entre partículas que influye directamente en el máximo de la fracción de volumen (o empaquetamiento). En un sistema de partículas esféricas monodispersas, el volumen máximo es alrededor del 64%. Sin embargo, esto también es efectivo al fluir alrededor de las partículas, recursos en posiciones de bajo volumen. El término «fluye fácilmente» se interpreta como una reducción de viscosidad. Alternativamente, pequeñas partículas facilitan el movimiento, actuando como lubricantes.

Fig 4 revela estos resultados interesantes. En un volumen fijo, la viscosidad del sistema polidisperso compuesto por partículas grandes y pequeñas puede ser menor que la viscosidad de cada una por separado. Existen dos efectos contrapuestos: uno ligado al número de partículas interactivas en función del tamaño y el efecto polidisperso.

  En los sistemas de recubrimiento, simplemente aumentar la polidispersión o la cantidad de aditivo permite mantener la viscosidad en un contexto dado, incluso tras el añadido de rellenos o pigmentos.

  El efecto polidispersión es un aspecto a considerar cuando un proveedor reemplaza aditivos en materiales de recubrimiento. Unidades de suministro emplean el mismo tamaño de partículas, de modo que la distribución no se ve afectada. Como resultado, no hay cambios en las características reológicas.Por ejemplo, usando un Mastersizer 2000 no solo se mide el tamaño de partículas, sino también su distribución.