Comprensión de los analizadores de partículas láser y principios de análisis de tamaño de partículas

Principios básicos del análisis de tamaño de partículas

¿Qué es una partícula?

Preguntar eso es una pregunta muy tonta. Sin embargo, en las diversas técnicas de análisis de tamaño de partículas, esto se convierte en la base. El proceso de dispersión y la forma del material se vuelven más complejos desde el principio en el análisis del tamaño de las partículas.

Problema del tamaño de las partículas

Supongamos que a alguien se le dio una caja de cerillas y se le preguntó cuánto mide.  

Probablemente dirían que el tamaño de la caja de cerillas es 20*10*5mm.  

No podrías decir exactamente que «el tamaño de la caja de cerillas es de 20mm», y esto sería una opinión sobre el tamaño. Así que no se puede describir una caja de cerillas tridimensional con una sola medida.  

Claramente, tales situaciones se vuelven más difíciles en formas complejas como partículas de arena o pigmento en una lata de pintura.  

Como gerente de control de calidad, me gustaría tener un solo número para describir las partículas; por ejemplo, conocer si el tamaño promedio del último lote de producción ha aumentado o disminuido. Este es un problema fundamental del análisis de tamaño de partículas: ¿cómo representamos un objeto tridimensional con un solo número? 

 
La Figura 1 muestra algunas partículas de arena. ¿Cuál es su tamaño? 

Esferas equivalentes 

Hay una esfera que se puede representar con un solo número. Si mencionamos una esfera de 50μm, esto se puede expresar con precisión. Al describir el borde y la diagonal de un cubo de 50μm, no se puede expresar. 

 Una caja de cerillas con muchas características puede representarse con un solo número. Por ejemplo, el peso con relación al volumen y la superficie es un número específico. Si hay una técnica para medir el peso de una caja de cerillas, podemos convertir el peso de la caja en el de una esfera. 

Es importante recordar 

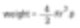
Y calcula un número específico (2r) sobre el diámetro de la esfera con un peso similar al de una caja de cerillas. Esto es la teoría de las esferas equivalentes. 

Suponemos una partícula calificada como una esfera y medimos ciertas propiedades de las partículas. Así, obtenemos un número específico (diámetro de esfera) para representar la partícula. 

Aunque puede ser incómodo usar varios números para describir una partícula tridimensional con precisión para fines de control, esto indica que no necesitamos más de 3 o más números. 

Podemos ver efectos interesantes que dependen de la forma del objeto, representados por un cilindro similar a una esfera. (Fig.2) 

Sin embargo, el volumen/peso cambiará si cambia la forma o el tamaño del cilindro. Y como un modelo de esfera equivalente, podemos decir que se hizo más pequeño o más grande. 

Diámetro equivalente de una esfera para un cilindro de 100 x 20μm 

Supongamos que el diámetro de un cilindro es D1=20μm y la altura es 100μm. Hay una esfera con el mismo volumen que el cilindro con un diámetro D2. Podemos calcular el diámetro de la siguiente manera. 

Volumen del cilindro  

Volumen de la esfera  

X es el valor del radio de volumen. 

El diámetro volumétrico de una esfera de un cilindro con altura de 100μm y diámetro de 20μm es aproximadamente 40μm. La tabla de abajo muestra los diámetros esféricos de varios cilindros en diferentes proporciones. La última fila mostraría partículas de arcilla grandes en forma de disco típico. No tendrías que considerar sus dimensiones generalmente debido a su grosor de 20μm y una altura de 0.2μm.  

En cuanto a herramientas para medir el volumen de partículas, podríamos obtener una respuesta de aproximadamente 5μm. Siendo así, sería necesario utilizar otras técnicas debido a la posibilidad de refutar este tipo de respuesta. 

Además, todos estos cilindros también pueden pasar como un filtro de 25μm de tamaño, y se podría decir que «todas las partículas son menores de 25μm». Aunque estos cilindros tienen valores diferentes, pueden parecer diferentes cuando se someten a la difracción láser. 

Diversas técnicas de medición

Obviamente, si observas una partícula a través de un microscopio, notarás que se proyecta en 2D, y hay varios diámetros de partículas que puedes caracterizar y medir. Si aceptamos la longitud máxima de la partícula y decidimos usarla como nuestro tamaño, podríamos decir que la partícula es una esfera que posee las dimensiones máximas. 

De manera similar, si usamos cantidades como el diámetro mínimo o el diámetro de Feter, esto nos proporcionará otra respuesta sobre el tamaño de la partícula. Por ello, es esencial reconocer que cada técnica puede medir diferentes propiedades de una partícula (longitud máxima, longitud mínima, volumen, área de superficie, etc.). En consecuencia, si una técnica es utilizada selectivamente, obtendrá resultados diferentes de otras técnicas de medición.

 
La Figura 3 muestra varias respuestas que pueden representar un grano de arena. Todas las técnicas están correctas, ya que todas miden diferentes propiedades de la partícula. Sería igual que medir una caja de cerillas en cm o pulgadas (¡tú mides la longitud y yo el ancho!). 

De esta forma, solo podemos comparar al medir en forma de polvo mediante la misma técnica. Esto significa que ninguna partícula de arena puede establecer un estándar de tamaño para todo. El estándar tiene que ser esférico cuando se compara entre diferentes técnicas. Sin embargo, se pueden obtener estándares de tamaño de partícula de cada técnica particular, lo que luego llevaría a comparar los equipos que usaron esas técnicas. 

D[4,3]

Imaginemos tres esferas con dimensiones 1,2,3. ¿Cuál sería el tamaño promedio entre las tres partículas? Primero, probablemente diríamos que es 2. ¿Cómo obtuvimos esta respuesta?   

Sumamos todos los valores y luego dividimos por el número total de partículas.   

Esto es un promedio por número (más precisamente un promedio en longitud). El número de partículas se puede representar en una fórmula. 

En términos matemáticos, se llama D[1,0]. La razón es que el término diámetro en la formula superior tiene orden 1, mientras que la fórmula inferior tiene orden 0. No obstante, si yo fuera ingeniero catalítico, preferiría comparar estas esferas con base en el área de superficie, porque un área de superficie mayor implica una mayor reactividad catalítica. 

La superficie de una esfera está dada por . Para compararlas basándonos en el área de superficie, es necesario sumar los cuadrados de los diámetros, y dividir entre el número total de partículas. Para volver al diámetro promedio, se utiliza la raíz cuadrada. 

Esto es nuevamente un promedio por número (promedio de números de superficie). La razón es que el número de partículas aparece en la fórmula inferior. Sumamos todos los cuadrados de los diámetros, y por eso en términos matemáticos se llama D[2,0]. La fórmula superior está elevada al cuadrado y el término diámetro es el inferior. Si yo fuera un especialista en química, querría comparar las esferas por su peso básico. La fórmula para el peso de una esfera es: 

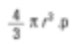
Y debes calcular los cubos de las dimensiones dividiéndolos por el número de partículas y para volver al diámetro promedio debes tomar la raíz cúbica.