This white paper examines the impact of particle properties on suspension viscosity, and more broadly on rheological behavior. It looks in some detail at how particle size, shape and zeta potential influence critical aspects of suspension performance such as viscosity and stability and how these properties can be manipulated to tailor rheological behavior.
Many products are suspensions or dispersions of particles in a liquid medium. Examples range from adhesives, ceramics, paints and inks through to foods, drinks, personal care products and medicines. The physical properties of the dispersed particles in such systems, including particle size, particle size distribution, concentration, electric charge (zeta potential), and even particle shape, can all strongly influence the overall (bulk) rheological properties of a suspension, thereby defining product behavior and functionality. Understanding these interactions is crucial when it comes to achieving desirable product performance, whether it be a stable paint or medicine, workable cement, or a visually appealing shower gel or drink.
This white paper examines the impact of particle properties on suspension viscosity, and more broadly on rheological behavior. It looks in some detail at how particle size, shape and zeta potential influence critical aspects of suspension performance such as viscosity and stability and how these properties can be manipulated to tailor this behavior.
At the start of his career Albert Einstein studied and described the flow field around a single hard sphere in a liquid [1, 2]. He concluded that single particles increased the viscosity of a liquid as a simple function of their phase volume, according to the formula.

Where
η – viscosity of the suspension
ηmedium – viscosity of the medium
ɸ – volume fraction of solids in the suspension
Einstein's conclusions remain of great value for describing systems containing very low particle concentrations but in many industrial suspensions particle loadings are relatively high, with particles in far closer proximity to one another. The consequence of this is a much more inhibited flow field that results in higher suspension viscosities and greater sensitivity to incremental changes in particle concentration. A number of semi-empirical models have been developed to account for this 'crowding' effect with the following model developed by Irvin Krieger and Thomas Dougherty perhaps the most popular [3-5].
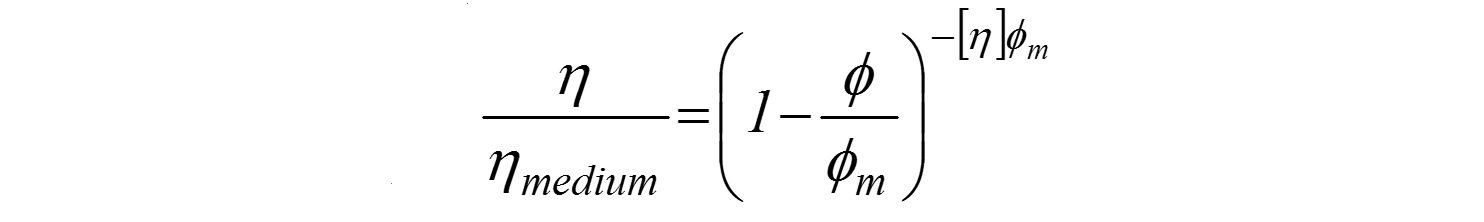
Where
ɸm – maximum vol. fraction of solids in the suspension
[η] – intrinsic viscosity (2.5 for spheres)
The Krieger and Dougherty relationship describes the relationship between particle loading or concentration and viscosity in this regime of higher particle concentrations and in addition to the parameters described in Einstein's equation includes an extra parameter, the maximum packing fraction, ϕm. This is the maximum volume of particles that can be added to a suspension before the system 'jams up' and viscosity becomes infinite.
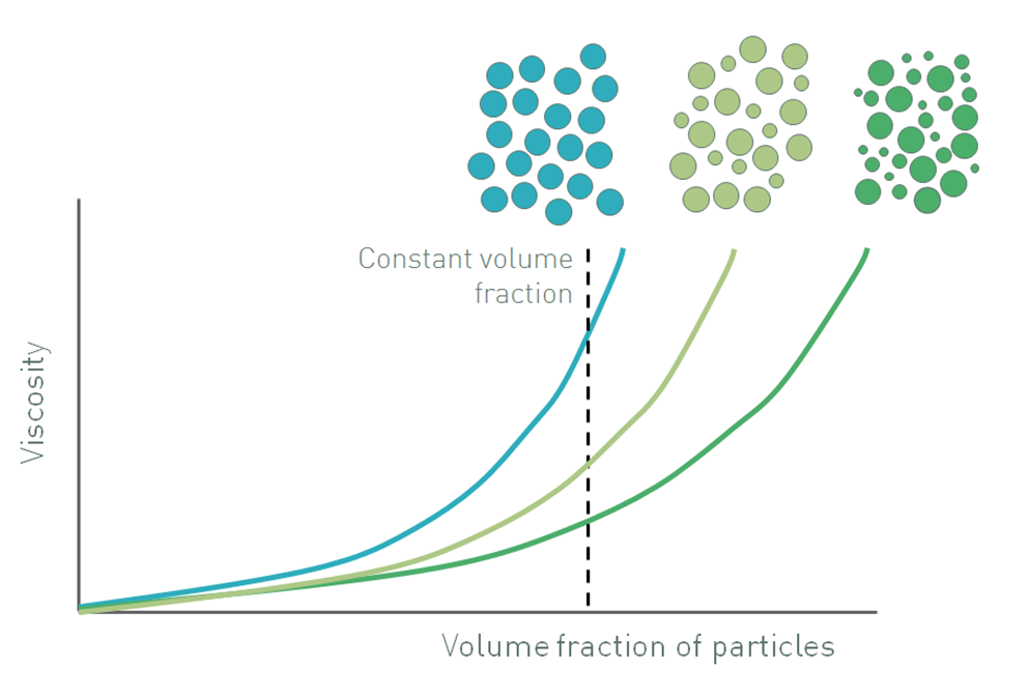
Figure 1: Increasing the volume fraction of particles in a suspension increases viscosity and also influences whether a suspension will exhibit Newtonian or non-Newtonian behavior
Figure 1 shows how the viscosity of a suspension changes as the volume fraction of particles is increased, relative to the maximum volume fraction. At low volume fractions, where ɸ/ɸm is less than 0.1, there is room for the particles to move freely, a situation closer to that considered by Einstein. The suspension exhibits the Newtonian response of the continuous phase which means that viscosity is independent of shear rate, but has a higher viscosity because the fluid has to circumvent the dispersed particles.
As the volume fraction increases, typically in a range of 0.1-0.5, particle-particle interactions start to become significant. These interactions inhibit the freedom with which particles move, and also influence fluid flow around adjacent particles, giving rise to an increase in viscosity. However, because the strength of particle-particle interactions is relatively low they are broken down as shear rate is increased. This effect is compounded by the influence of Brownian motion, especially in suspensions containing fine particles, where Brownian stresses can be relatively high. Brownian motion opposes an applied shear stress, acting to maintain randomized particle movement. This effect is overcome at higher stresses when particles are able to rearrange into a more efficient packing structure by forming rafts and strings [4, 5]. Both mechanisms contribute to non-Newtonian, shear thinning behavior, where viscosity is no longer independent of shear rate or shear stress (Newtonian) but decreases as shear is increased.
At even higher particle loading, once ɸ/ɸm exceeds approximately 0.5-0.6, there is minimal room for the particles to move and the flow field around particles becomes much more complex. Now the particles are not only interacting with each other, they are physically inhibiting the motion of one another with the fluid playing more of a lubricating role. As shear increases this inhibition of movement becomes more and more limiting and the suspension can exhibit shear thickening behavior, where viscosity increases with shear rate, due to particle jamming or formation of particle clusters. The actual figures of ɸ/ɸm that mark the transition from Newtonian to shear thinning and then to shear thickening behavior are system specific but those included here provide a good guideline in most cases. The shear rate or shear stress at which shear thickening occurs is also system dependent [5].
If volume fraction is kept constant, then decreasing particle size leads to an increase in the number of particles present. This is especially the case with sub-micron sized particles. For such particles the effective hydrodynamic size may be substantially increased by any surface charge, hydration or adsorption layers that surround each core particle. This will result in a higher effective volume fraction for a given particle loading, thereby increasing the viscosity of the suspension. For larger particles which are fewer in number this effect is greatly reduced.
Figure 2 shows data for latex particles in a pressure-sensitive adhesive that illustrate this effect. Because inter-particle (colloidal) interactions are dominant at low shear rates, the effect is more pronounced in this range with smaller particles giving higher viscosities due to their higher effective volume. At high shear rates inter-particle forces are broken down and hydrodynamic forces dominate. A consequence of this is that the effective volume fraction becomes less dependent on particle size and viscosity values converge.
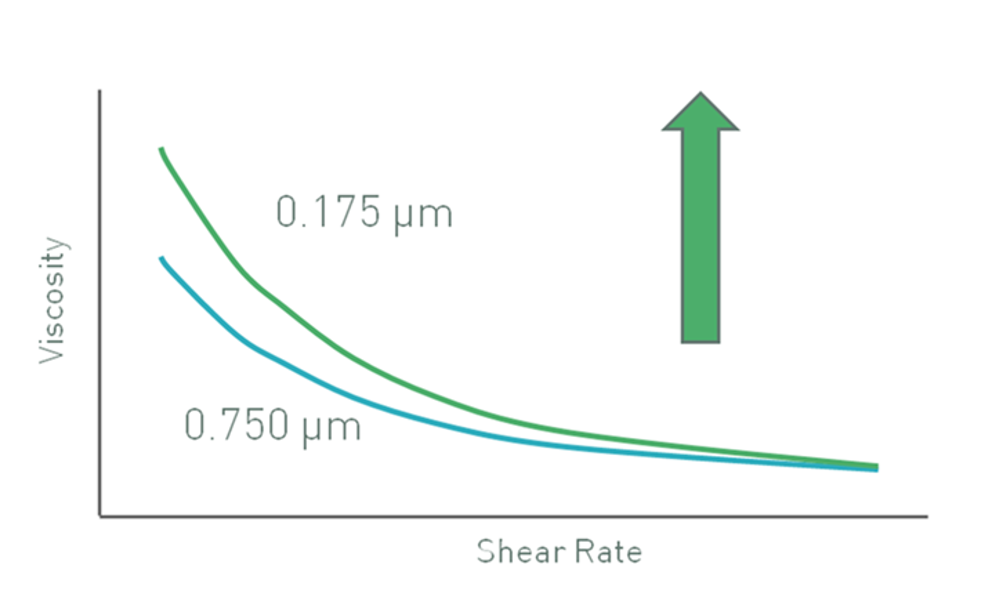
Figure 2: Decreasing particle size may lead to an increase in low shear viscosity, for a constant volume fraction of particles, if colloidal interactions are significant
Brownian motion is another important factor since this opposes any applied shear stress and is particle size dependent. Consequently, the onset of shear thinning occurs at higher shear rates or stresses for smaller sized particles.
Polydispersity is the span or range of the particle size distribution. A particle size distribution with a wide span contains dissimilarly sized particles – large and small - which can pack more efficiently than a collection of monodisperse particles, providing more free space and making it easier for an equivalent volume of particles to move around, hence lowering viscosity. In terms of the Krieger-Dougherty relationship this increase in polydispersity increases the maximum volume fraction thereby lowering viscosity. Conversely this means that narrowing the particle size distribution can increase viscosity, a change often associated with increased stability.
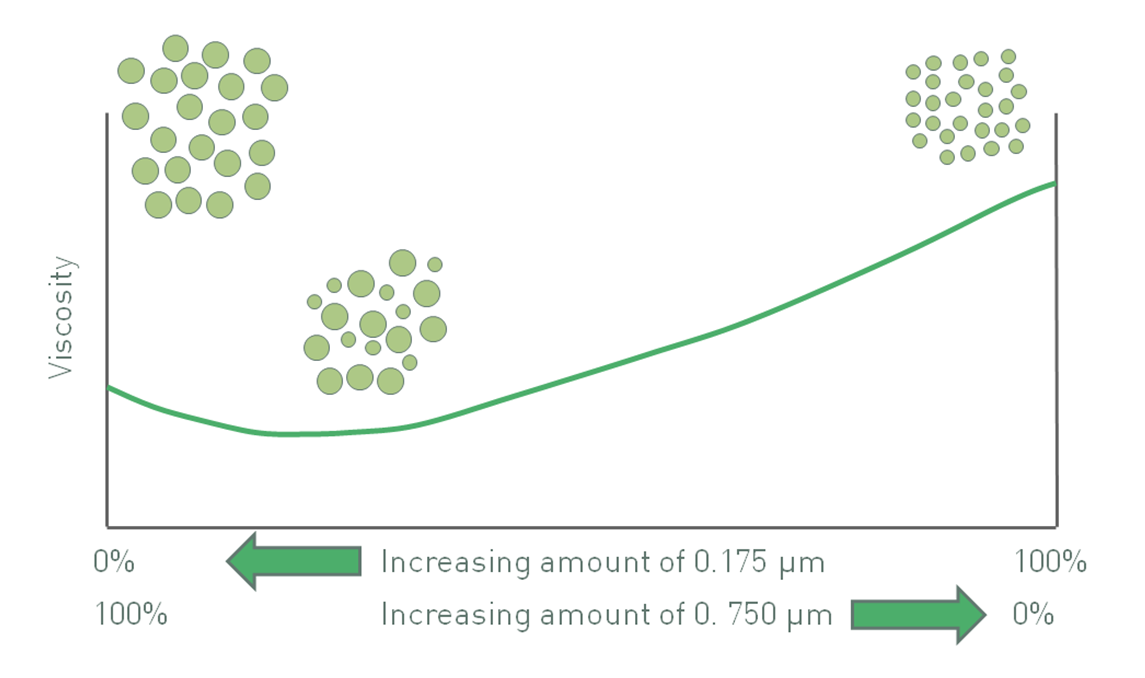
Figure 3: The impact of polydispersity and particle size can produce competing effects and in the system above produces a minimum viscosity value
The effects of polydispersity and particle size can at times be competing, so particle size and particle size distribution can be used in combination to control viscosity. Returning to the example of using either 175 nm particles or 750 nm particles (see figure 2), a bimodal distribution of these two particles results in a minimum viscosity (see figure 3). For a given volume fraction, suspension viscosity with only 750 nm particles is lower than with 175 nm because the use of finer particles increases the effective volume fraction. However, the inclusion of a relatively small fraction of 175 nm particles to make a binary mixture, reduces rather than increases viscosity. The impact of these finer particles on packing behavior, an effect that decreases viscosity, more than offsets the increase in viscosity caused by a greater number of particle-particle interactions.
Convexity is a measure of the regularity or sharpness of the perimeter of a particle, a descriptor of particle shape. Particles with low convexity (see figure 4) have a convoluted outline that increases the likelihood of mechanical resistance to flow in a suspension. Furthermore, relative to equivalently sized smooth particles, particles with low convexity may have a high specific surface area, increasing the number of particle-particle interactions and any related chemical interactions. Both effects tend to be more marked at high solids loadings. Even at lower volume fractions, higher particle roughness or irregularity can cause an increase in viscosity due to the deviation of liquid flow around them. Taking in to account all of these effects the viscosity of a suspension can often be reduced by using smoother, more regular particles, although once again any impact is usually more marked at low shear rates and high volume fractions.
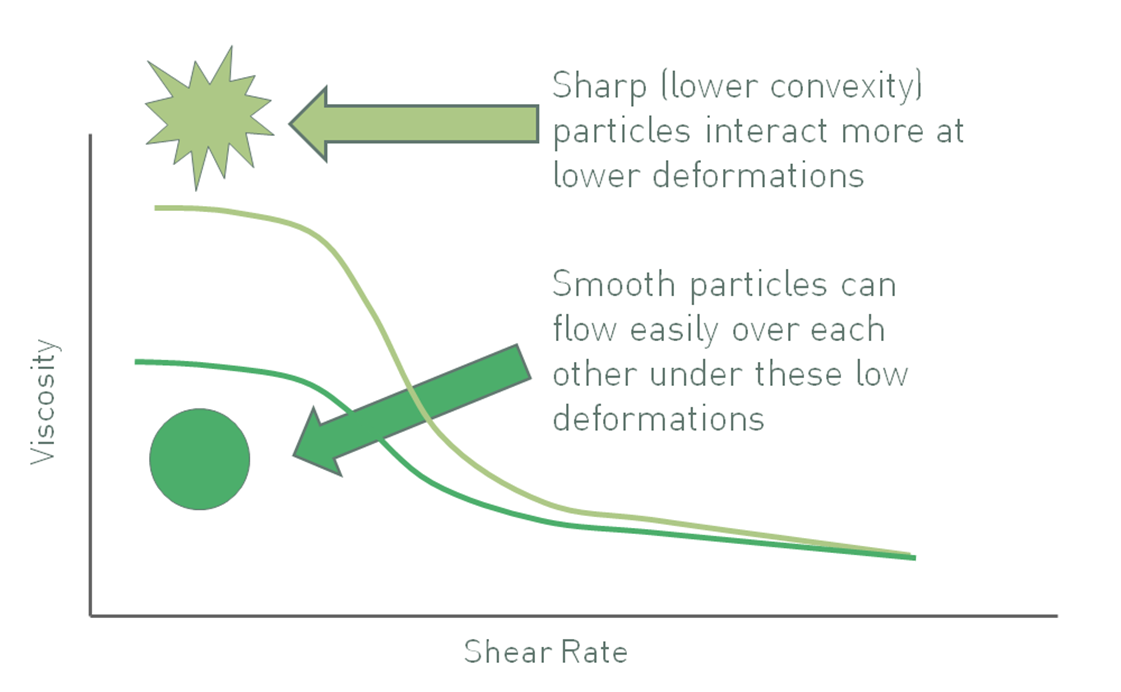
Figure 4: Sharper particles, those with lower convexity, give rise to suspensions with higher viscosity, all other factors being equal
Elongated particles produce a different suspension viscosity profile to spherical analogues. Particle-particle interactions between spherical particles typically break down as shear increases, and this gives rise to shear thinning behavior. Elongated particles randomly orient at low shear, thus occupying larger volumes, but at high shear will tend to orient in the direction of flow resulting in more efficient packing. As a result, suspensions with elongated particles also shear thin, but far more markedly that those containing spherical particles. In terms of the Krieger-Dougherty expression, particle irregularity increases the intrinsic viscosity [η] relative to that of a sphere and reduces the maximum packing fraction, which gives a higher low shear viscosity.
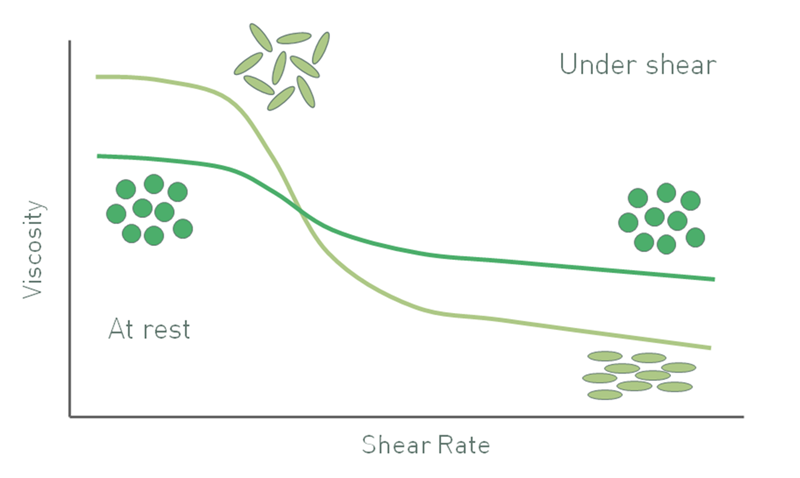
Figure 5: As a result of orientation at high shear rates the viscosity of suspensions with elongated particles has a different profile from that of a suspension containing spherical particles of equivalent size
The preceding analysis of how particle size and shape impact viscosity has shown that these physical characteristics influence how easily particles within a suspension can move, relative to one another. One further parameter that also influences particle movement, and consequently viscosity and stability, is the electrical charge on particles within a system. One way of measuring this charge is to quantify zeta potential.
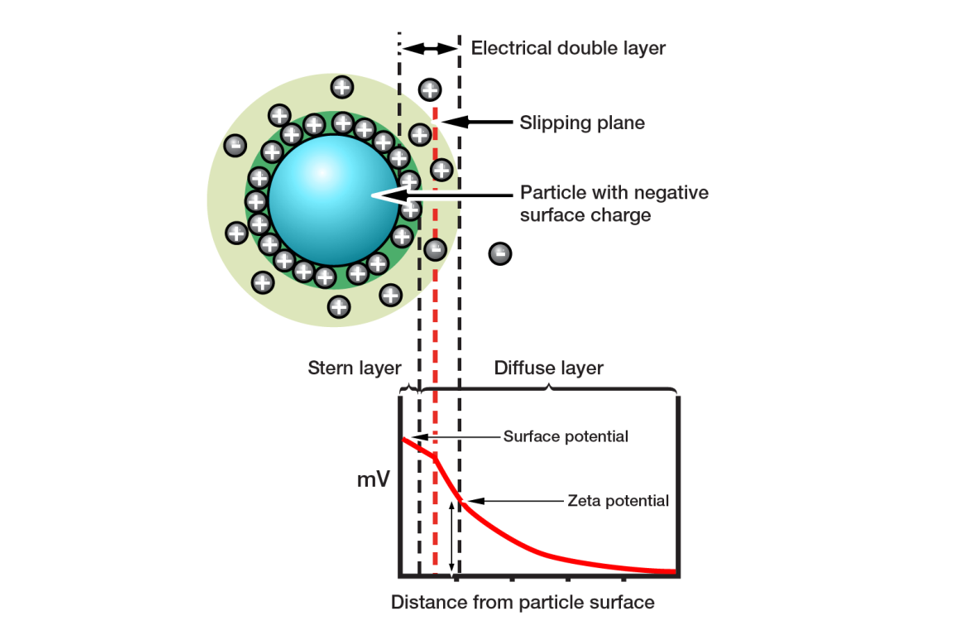
Figure 6: Zeta potential influences whether particles will repel or attract when held in suspension
Zeta potential quantifies the magnitude of the electrostatic repulsion or attraction in a system. It is a measure of particle charge at the edge of the slipping plane between the particle and associated double layer, and the surrounding solvent (see figure 6). The fact that zeta potential is not the charge on the surface of the particle, but rather at the edge of the particle’s ‘sphere of influence’, makes it highly relevant to suspension behavior. If a suspension has a large negative or positive zeta potential, then the particles within it will tend to repel each other. Low zeta potential values increase the likelihood of flocculation or agglomeration, the joining together of discrete particles.
In colloidal systems particles tend to move under Brownian motion and the influence of gravity is low because particle mass is small. Here, increasing the zeta potential causes particles to repel one another, inhibiting movement and increasing viscosity, especially at low shear rates (see figure 7) when the particles exhibit a larger effective hydrodynamic volume due to their charge. A zeta potential of sufficient magnitude, around ±30 mV, will maintain particle separation. In these systems gravitational forces only become large enough to cause sedimentation if the particles grow in mass by a process of agglomeration. Keeping particles separate therefore ensures stability [6].
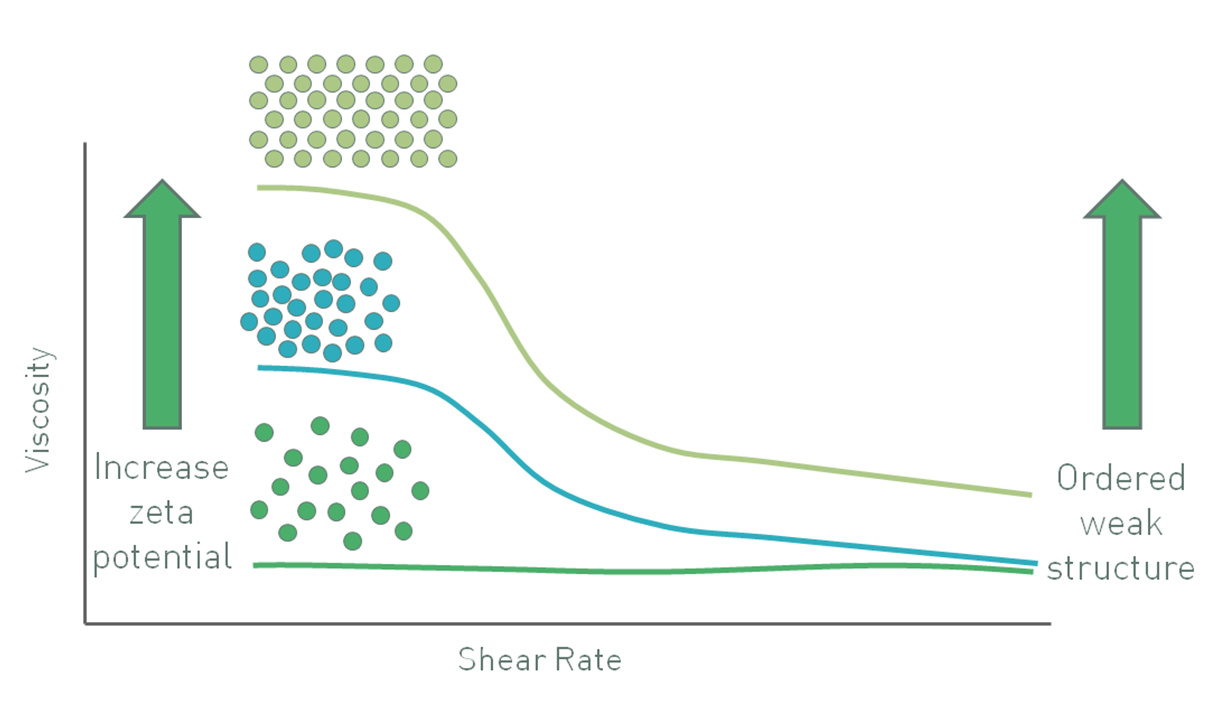
Figure 7: In a colloidal suspension with sub-micron particles increasing zeta potential increases viscosity at low shear stress through an increase in the particles effective phase volume
In a suspension with larger particles, zeta potential may be controlled in order to deliver a quite different effect. For particles of significant mass, gravitational forces are sufficient to induce sedimentation. Here, engineering a high zeta potential to maintain the particles as discrete entities does not produce a stable suspension. Counter-intuitively, the opposite can work. In certain systems reducing the zeta potential induces partial agglomeration of the particles, creating a networked gel that can give appreciable viscosity to a suspension, and induce an apparent yield stress (Figure 8) [6].
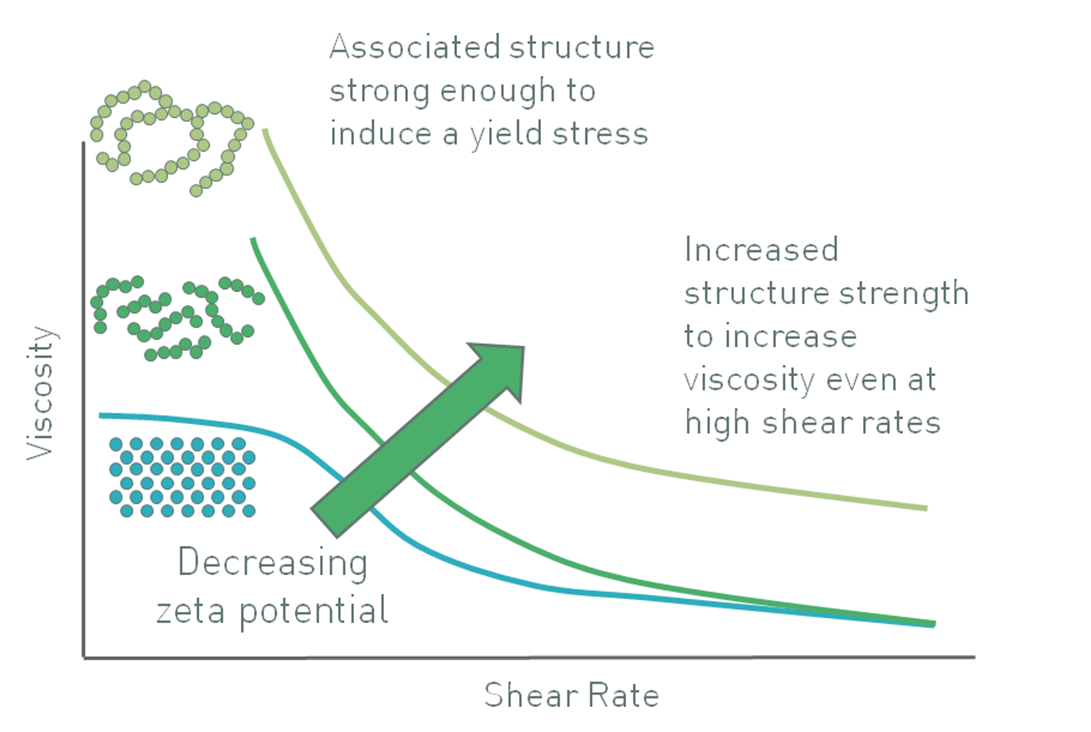
Figure 8: Decreasing zeta potential can induce a flocculated particle gel with an apparent yield stress that enhances stability
Clearly a number of strategies can be used to refine rheological properties to meet performance targets for a specific suspension. However, the driver for such formulation optimization is analytical data. Laser diffraction and dynamic light scattering (DLS) are well-established techniques for measuring particle size distributions centred in the micron and sub-micron ranges, respectively. Zeta potential can be measured by electrophoretic light scattering, a technique that is complementary to DLS and often integrated in dynamic light scattering systems, while automated imaging brings rapid, statistically relevant particle shape analysis.
For rheological measurements, rotational rheometers are arguably the most versatile rheological tools available and can be configured for a number of different rheological methods, to probe the structure and performance of suspensions. Test types range from the generation of viscosity flow curves over many decades of shear stress and shear rate, through to measurements of yield stress, thixotropy and viscoelasticity.
Capillary rheometry is useful for measuring the viscosity profiles of suspensions and slurries containing relatively large particles, at high particle loadings. Industrial examples include powder injection molding, ceramic slurries, foodstuffs, inks and coatings. Capillary rheometers can apply very high force, which enables the exploration of behavior at far higher shear rates than is possible with rotational rheometry, such as those associated with extrusion and injection.
1. Einstein A (1906), Eine neue Bestimmung der Molek ¨ uldimensionen. Ann Physik. 19 289-306.
2. Einstein A (1911), Berichtigung zu meiner Arbeit: "Eine neue Bestimmung der Molek¨ uldimensionen." Ann Physik. 34 591-2.
3. Krieger IM; Dougherty TJ, A mechanism of non-Newtonian flow in suspensions of rigid spheres. Trans Soc Rheol. 3 (1959), 137
4. Barnes HA, Hutton JF and Walters K (1989), An Introduction to Rheology
5. Mewis J, Wagner NJ (2012), Colloidal Suspension Rheology
6. Suspension Stability Suspension Stability; Why Particle Size, Zeta Potential and Rheology are Important – Malvern Panalytical application note “http://www.malvernpanalytical.com/en/support/resource-center/application-notes/AN101130SuspensionStability.aspx”