What is the Mark-Houwink equation – and how do you use it for polymer characterization?

了解聚合物的分子結構對於預測其性質和調整其性能至關重要。馬克-霍因克方程式（有時也稱為馬克-霍因克-櫻井方程式）是高分子科學家用來獲得這種理解的最強有力的工具之一。

通過將本徵黏度與摩爾質量相關聯，馬克-霍因克方程式解鎖了對聚合物架構的見解，且當其通過 使用 尺寸排除色譜（SEC）結合多角光散射（SEC-MALS）和黏度法驗證時，特別強大。

憑藉這些精確的見解，石化專業人士可以微調其聚合物的性質，以確保其達到精確的規範和法規要求。

在本博客中，我們將介紹馬克-霍因克方程式是什麼以及如何使用 SEC-MALS 增強其見解，並展示馬克-霍因克圖在實際應用中的例子。無論您是在研發新的塑料等級，分析生產中的聚合物，還是監督質量控制，這就是該方程式如何能幫助您的方法。

馬克-霍因克方程式是什麼？

馬克-霍因克方程式描述了一種聚合物的本徵黏度（η）與其分子量（M）之間的經驗關係：

[η] = K · M^a

它有四個關鍵組成部分：

1. [η]: 本徵黏度。這是衡量聚合物溶解於液體後增加該液體黏度的程度。
2. M: 分子量。這是一個分子的總重量——對於聚合物來說，它指的是聚合物鏈的重量，這指示了鏈接在一起的單體單元數量。
3. K 和 a: 這些是依賴手頭聚合物類型和你正在使用的溶劑的常數。

馬克-霍因克方程式之所以有用，是因為它可以幫助您根據溶液的本徵黏度計算分子量；反過來，它可以幫助您預測根據其分子量將有多黏的聚合物溶液。它還可以讓您洞察結構信息，例如分支和鏈硬度。

馬克-霍因克方程式中的 K 和 a 是什麼？

在馬克-霍因克方程式中，K 和 a 是描述您的聚合物本徵黏度與其分子量關係以及聚合物在溶液中的形狀的常數。

K 常數決定了本徵黏度與分子量之間的關係。它取決於：

• 聚合物的類型
• 它溶解的溶劑
• 溶液的溫度

更大的 K 值意味著即使是小的聚合物分子也會顯著增加溶液的黏度；小的 K 值意味著每單位質量，聚合物對黏度的影響較小。

K 值可以有很大差異，通常在聚合物數據表中列出。如果沒有，則必須通過實驗測量。這通常通過使用如 SEC-MALS 等絕對方法測量本徵黏度和分子量，然後將數據適合於馬克-霍因克方程式來完成。

a 告訴您關於聚合物在溶液中的形狀：

• 如果 a 約為 0，則聚合物具有緊湊或球狀結構，如形成緊密線圈。
• 如果 a 在 0.5 和 0.8 之間，則聚合物呈現隨機線圈結構。
• 如果 a 超過 1，則聚合物抗拒盤繞並形成剛性的棒狀分子。

馬克-霍因克方程式用於什麼？

馬克-霍因克方程式用於創建馬克-霍因克圖，該圖將 log[η] 對 log(M) 繪製。這些圖使科學家能夠：

• 比較聚合物架構
• 檢測分支或結構變化
• 分析分子量一致性

例如，這裡是苯乙烯和PMMA在馬克-霍因克圖上的比較。由於PMMA具有更緻密的分子結構，因此在圖中出現較低的位置：

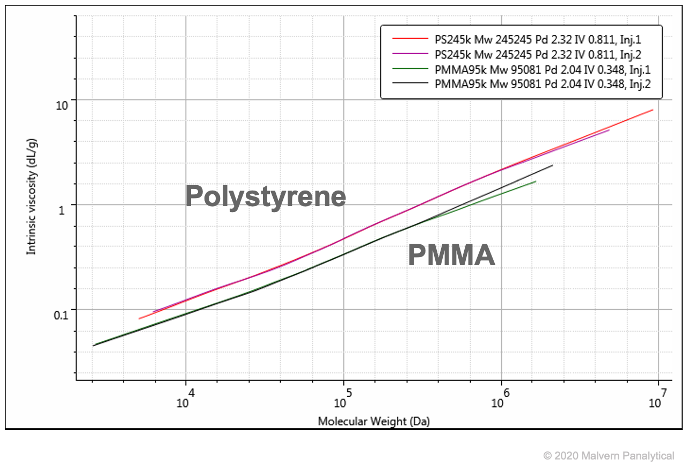
您可以看到下方更多馬克-霍因克圖的例子。

如何計算馬克-霍因克方程式中的 K 和 a 值？

如果您不知道您的聚合物和溶液組合的K 和 a 值， 或者想要將您的方法精確驗證或校准到您的材料，您必須通過實驗測量它們。 這可以通過 SEC 完成，通常結合 SEC-MALS 。

使用像 Malvern Panalytical 的 OMNISEC 這樣的 SEC-MALS 儀器，加上一個黏度計，您可以查看本徵黏度 [η] 和分子量 (M) 如何跨越整個分子量分佈的樣本變化，而不僅僅是在平均點。

這在表徵新聚合物和精簡未來的質量控制方法時特別有用。取代在日常 QC 中重複深入分析，您可以根據材料的證明本徵黏度值快速估計樣本的分子量。

馬克-霍因克方程式在實踐中的例子：從我們的分析中獲得見解

了解馬克-霍因克方程式如何實際使用，特別是當與 SEC-MALS 技術結合時，最好是查看真實案例。以下是使用我們的儀器應用馬克-霍因克方程式的三個例子。

1. 通過結合 APC 和 OMNISEC REVEAL 來揭示聚合物結構

在這項研究中，我們結合了 Waters ACQUITY 先進聚合物色譜 (APC™) 與我們的 OMNISEC 多檢測儀器來比較苯乙烯、聚碳酸酯和聚氯乙烯 (PVC)。然後，我們將這些材料的分子量分佈輸入馬克-霍因克圖以揭示：

• 苯乙烯具有最低的本徵黏度，暗示其結構緊湊且密集。
• 聚碳酸酯顯示出更高的本徵黏度，意味著其結構更加開放，密度較低。
• PVC 在高分子量時並不遵循線性模式，暗示有分支發生——這一發現若無多檢測 SEC 將無法可見。

在這裡閱讀完整研究。

2. 將葡聚糖樣本與其他多醣進行比較

葡聚糖是一種多醣，常用於醫療領域，例如用於眼藥水潤滑劑和靜脈注射溶液成分，這些成分有助於防止血液凝結。在這些藥用應用中，每個葡聚糖樣品的分子量和本徵黏度決定了其行為和潛在副作用。因此，在將這些材料用於藥品之前，準確表徵這些材料是很重要的。

我們使用我們的 OMNISEC 三檢測系統分析了分子量範圍從約 1 kDa 到超過 650 kDa 的葡聚糖樣本的結構一致性，並將其與另外兩種生物聚合物：阿拉伯膠和果膠進行比較。馬克-霍因克圖顯示：

• 葡聚糖樣本顯示出結構一致性。
• 阿拉伯膠在葡聚糖線下方，這意味著它比葡聚糖更密集。
• 果膠坐在葡聚糖線上方，顯示其更高的黏度——這是這種凝膠劑所期望的屬性。

在這裡閱讀完整應用說明。

3. 修改雙模聚合物的骨架

最後，我們提交了一個雙模聚合物進行了四個階段的骨架修改，並使用馬克-霍因克圖鑑別修改的成功。 我們的研究發現：

• 最初，在比較起始材料和最終產品時，有兩條明顯的馬克-霍因克線，顯示兩種結構群體的存在。
• 經過每次修改步驟後，本徵黏度增加，尤其是在低分子量範圍的峰值。
• 最終結果是在馬克-霍因克圖上形成一條線，表示結構一致的最終產品。

在這裡查看完整的應用說明。

結合馬克-霍因克方程式與精確分析進行完整的聚合物表徵

對於跨研究和開發、過程管理和質量控制的石化專業人士來說，馬克-霍因克方程式是驗證您的分析和簡化流程的寶貴工具。

如需增強您的計算，探索我們的OMNISEC解決方案系列：世界上最先進的多檢測器 SEC 系統。

進一步閱讀

• What is the Mark-Houwink equation – and how do you use it for polymer characterization?
• Optimizing XRD throughput with the Aeris High-Capacity Sample Changer: Key insights from our webinar
• 如何測試水中的微塑料
• 探索聚合物表徵（第一部分）：技術及其影響