粒度分析の基本原理-1

ダウンロード



粒度分析の基本原理 

粒子とは？

  それを尋ねることは非常に愚かな質問である。しかし、様々な粒子サイズ分析技術において、このようなものが基礎となる。分散過程と材料の形状は、粒子サイズ分析において、初めよりもさらに複雑になっている。

粒子サイズの問題

  マッチ箱を渡し、誰かがそのマッチ箱のサイズを教えろと言ったと仮定してみよう。おそらくこのマッチ箱のサイズが20*10*5mmだと答えるだろう。”マッチ箱のサイズが20mmです”と正確に答えることはできず、これがサイズを説明する一つの見解と言える。それであなたは一つの固有寸法では立体的なマッチ箱を表現することができない。明らかにこのような状況は、砂粒やペンキ缶内の色素粒子といった複雑な形状ではさらなる困難をきたすことになる。もし私がQ.A.(品質管理)マネジャーなら、粒子の描写に一つの数字を求めるだろう – 例えば最後に作った製品の平均サイズが増加しているか減少しているかを知りたいと思うだろう。これは粒子サイズ分析における基本的な問題である – どのように一つの数字で立体的な物体を表現するのか？

相当球(Equivalent spheres)

  一つの唯一の数字で表現可能な球がある。もし私たちが50μmサイズの一つの球を言及する時、これは正確に表現可能である。50μmサイズのキューブのエッジや対角線を言及する時、それは表現することができない。多くの特徴を持つマッチ箱は一つの数字で表現可能だ。例えば、体積や表面積に関連する重さは一つの特定した数字だ。もしマッチ箱の重さを測定する技術があれば、私たちはそのマッチ箱の重さを球の重さに変換することができるだろう。 

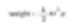
  記憶に留めておくべきは、そしてマッチ箱と同じ重さの球の直径について一つの特定数(2r)を計算する。これがequivalent sphere理論である。私たちは何らかの粒子の性質を測定し、球として言及された粒子を仮定する。それゆえ、粒子を表現するための一つの特定数(球の直径)を得ることになる。

   これは立体物を表現する際、たとえ制御目的のためにはより正確なことが不便である可能性があるが、3またはそれ以上の数で表現する必要はないということを示している。

   これが物体の形状に依存する興味深い効果を知ることができ、例として球のようなシリンダーを示した。

  しかしながら、もしシリンダーの形状やサイズが変わるならば体積/重さは変わるだろう。そして等価球形モデルにおいて、私たちは少なくともそれが小さくなったか大きくなったかを言うことができる。

100 x 20μmシリンダーの相当球(Equivalent spherical)直径

  シリンダーの直径がD1=20μm、高さが100μmと考えてみよう。直径がシリンダーと体積が同じD2の直径を持つ球がある。次のように直径を計算できる。

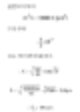
  100μm高さで20μm直径のシリンダーの球形体積の直径は約40μmである。下記の表は様々な比率のシリンダーの球形直径を示している。最後の行は典型的なディスク形状の大きな粘土粒子となる。それは高さ20μmで0.2μmの厚さを持つため、一般的に寸法を考慮しないで良い。粒子の体積を測る装置に関して、私たちは約5μm程度の答えを得るかもしれない。したがってこのような答えに対しては異議を唱える可能性があるため、別の技術を使用する必要がある。

  また、これらすべてのシリンダーは25μmのフィルターと同じサイズで表示され、「すべての材料は25μm未満である」と言えるかもしれない。これらのシリンダーはいずれも異なる値を持っているため、レーザー回折では異なって見える可能性がある。

さまざまな測定技術

  明確に言えば、もし顕微鏡を通して粒子を見たら、2次元で投影されたものを見ることができ、粒子を特徴化して測定できる粒子の直径がある。もし私たちが粒子の最大長さを受け入れてこれを私たちのサイズとして使用するならば、私たちは粒子が最大の寸法を持つ球粒子だと言うことができる。同様に、もし私たちが最小の直径やFeter’s diameterのような量を使用するならば、これは粒子の大きさについて別の答えを提供するだろう。このため、各技術は粒子の異なる物性(最大長、最小長、体積、表面積など)を測定できることを必ず知っておくべきである。したがって、選択的に測定するならば、残りの測定技術と異なる結果を示すだろう。

  Fig 3は一粒の砂を表現するのに役立つ他のいくつかの解決策を示しています。各技術は間違ってはいません – 技術はすべて正しく、粒子の異なる性質を測定しています。それはcmやインチ法でマッチ箱を測るようなものです(あなたが長さを測って、私は幅を測る！)。

  このようにして私たちはオーダーが同じ技術で測定したものと比較するしかありません。これは砂の粒のようなものでは標準のサイズで何もできないことを意味します。スタンダードは各技術間での比較を通じてのみ球形であるべきです。しかし、私たちはそれぞれの技術で標準的な粒子サイズを得ることができ、これにより技術を使用した装置の比較を行うことになります。

D[4,3]等

  1,2,3単位の寸法を持つ3つの球があると考えます。その三つの粒子間の平均サイズはどうなるでしょうか？最初に私たちはおそらく2と言うことでしょう。どうやってこの答えに至ったのでしょうか？私たちはすべての値を足して総粒子数で割るでしょう。

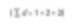
 これは数平均です(より正確には長さ平均の数です)。粒子の数は式で表現することができます。

  数学的な用語でD[1,0]と呼ばれます。理由は、上の方程式の直径項には(d1)がたくさんあり、下の方程式には直径項(d0)がないからです。けれど、私が触媒関連の工学を学んでいると想定してみると、表面積に基づいてこうした球を比較したいと思うでしょう。その理由は、より大きな表面積がより高い触媒の反応性を持っているからです。球の表面積は4πr^2です。したがって、表面積基準で比較する場合、私たちは粒子数で割った直径の二乗を求めなければなりません。そして、平均直径に戻るためには平方根を取る必要があります。

  これは再び数平均( 表面数平均)です。理由としては、式には粒子数が現れるからです。半径の二乗をすべて足します。これにより数学的にD[2,0]と呼ばれます。- 式の上の項は二乗しており、直径項は下にあります。もし私が化学専攻者であれば、基礎重量の球を比較したいと思うでしょう。球の重さの式は以下の通りです。

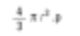
  そして係数で割った正方形インデックスを見つけ、平均直径に戻るために立方根を取る必要があります。

  これもまた数平均(数-体積または数-重量平均)で割ります。理由は、粒子数が式に現れるからです。数学的にこれはD[3,0]と表現できる。

  D[1,0],D[2,0],D[3,0]簡単な平均の問題点は、粒子数が式に関して固有であることです。これは多くの粒子を計算する必要が出てきます。計算する粒子は汚染、制御、清潔といった適用において低数(ppmやppb)の場合にのみ一般的に実行されます。もしシリカ1g(密度2.5)のサイズがすべて1μmであるならば、簡単な計算でそれらは約760*10^9粒子が存在することを示しています。

したがって、瞬間平均の概念は補充される必要があり、これは混乱を引き起こす可能性があります。重要な2つの平均値は次のとおりです。

• D[3,2]- 表面積平均 – Sauter平均直径
• D[4,3]- 体積または質量平均 – De Brouckere平均直径

  これらの平均は、慣性モーメントに似ており、別の直径に関連する線形な用語を導入します。(以下のように表面積はd3と相関があり、体積と質量はd4と相関があります。)

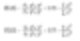
  これらの式は、頻度(表面積または体積/質量)分布の中心が回転することを示しています。実際には、それらは各分布の重心になります。この計算方法の利点は明らかです – 式には粒子数を含まないため、平均の計算と分布は、複雑な粒子の数に関する知識を必要としません。レーザー回折は最初に体積項を基にした貢献を計算し、これはD[4,3]がはっきりとした方法で報告されている理由だからです。

測定技術が異なれば、測定結果も異なる

  もし私たちが直径を測定したい粒子を測定するために格子線が付いた電子顕微鏡を使用するならば、平均結果を得るためには粒子の数で割るかすべてを足します。