The Z average is the intensity weighted mean hydrodynamic size of the ensemble collection of particles measured by dynamic light scattering (DLS). The Z average is derived from a Cumulants analysis of the measured correlation curve, wherein a single particle size is assumed and a single exponential fit is applied to the autocorrelation function.
The DLS autocorrelation function, along with the exponential fitting expression, is shown below, where I is the scattering intensity, t is the initial time, τis the delay time, A is the amplitude or intercept of the correlation function, B is the baseline, D is the diffusion coefficient, q is the scattering vector, λo is the vacuum laser wavelength, ñ is the medium refractive index, θ is the scattering angle, k is the Boltzmann constant, T is the absolute temperature, η is the viscosity of the medium, and RH is the hydrodynamic radius.
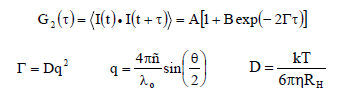
In the Cumulants approach, the exponential fitting expression is expanded to account for polydispersity or peak broadening effects, as shown below.
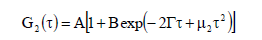
The expression is then linearized and the data fit to the form shown below, where the D subscript notation is used to indicate diameter. The 1st Cumulant or moment (a1) is used to calculate the intensity weighted Z average mean size and the 2nd moment (a2) is used to calculate a parameter defined as the polydispersity index (PdI).
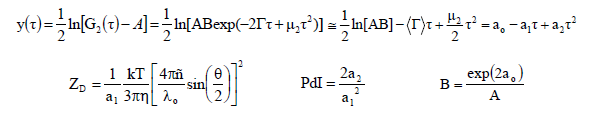
It is important to note here, that the Cumulants analysis algorithm does not yield a distribution – it gives only the intensity weighted Z average and the polydispersity index.
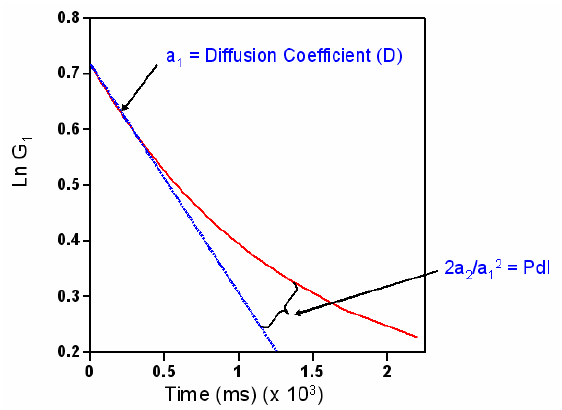
The figure below shows a graphical representation of the procedures employed within the Cumulants analysis to calculate the Z average and polydispersity index.
The initial slope (blue) of the correlation function is related to the z-average size, the curvature (red) indicates the nonlinearity due to the width of the polydispersity.