Basic Principles of Particle Analysis-2

Download



Number Distribution and Volume Distribution 



  The above example comes from New Scientist (October 31, 1991). There are large numbers that are designated by humans for the purpose of orbiting the Earth’s orbit regularly in space. Scientists also classified groups based on their size. If we examine the third paragraph above, we can accurately deduce that exactly 99.3% of all particles are incredibly small. This is an evaluation of data based on numbers. However, if we examine the fourth paragraph, we can accurately infer that virtually all objects are between 10-1000cm. This is the mass of all objects. The distribution of number and mass is very different and we must note that our conclusions may vary depending on the distribution we use. And neither distribution is accurate. Data is simply investigated in a different way. For example, if we are designing spacesuits, we might say it is easy to avoid 7000 large objects and care for 99.96% of all cases. However, the most critical aspect of a spacesuit is to protect against the 99.3% of small particles by number. If we calculate the average of the distributions in the table above, we should know that the number average is about 1.6cm and the mass average is about 500cm. – The difference is significant.

Conversion between Number, Length, Volume/Mass Distribution

  If we measure particles by electron microscope, we can see that we are calculating D[1,0] or the number-length average size from the previous content (different techniques provide different averages). If what we really require is the average size of mass or volume, we must convert the number average to a mass average. Mathematically, this is easily feasible, but we have to measure the result of such conversions.

  Consider that the electrical measurement technique takes a 3% error at average size. When we convert the number average size to mass average size, the mass average becomes a cubic function of diameter, at which point the error becomes the cube of the last value or 27%.

 











  However, the situation would change if we calculate the mass or volume distribution with laser dispersion.

  Under the recirculation conditions of the solution dispersion method, it would generate a reuse volume average of 0.5%.

  Now if we convert this volume average to a number average, the error or number average will be the cube root of 0.5%, less than 1.0%.

  Practically, if we want a volume or mass distribution by using an electron microscope, missing or losing one 10μ particle equals missing or losing one thousand 1μ particles. Hence, we must recognize the significant dangers of interconversion.

  Both DOS and Windows software calculate different diameters in Malvern Sizers. However, we must be cautious when obtaining these diameters. Different methods (meanings) can be converted by the equations appearing next, the Hatch-Choate equation – Ref.7.

 

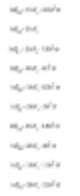
Measurement and Derived Diameter

  We have seen that Malvern laser diffraction technology leads to volume distribution for light energy data analysis. (It is noted that the area distribution investigated by Fraunhofer analysis is assumed.) This volume distribution can be converted into any number or diameter length as shown above.

  However, under some analytical techniques, we must be aware of the converted results (mutual conversion between number, length, and volume/mass averages in the previous section), and we must also understand that the average diameter is actually measured by the machine, and certain diameters are actually calculated or derived from the first measured diameter.

  Other techniques can obtain other diameters from some already measured diameters. For instance, the microscope will measure D[1,0] and from it derive other diameters.

  We can rely more on measured diameters than on derived ones. In actuality, relying on characteristics derived (computed) in several real (installation) cases may be very risky. For example, the Malvern analysis table presents us with a specific surface area (m/cc or m/gm).

  We should not fully accept the table. – Actually, if what we really want is the specific surface area of a material, there are special techniques for calculating surface area that we must use, like B.E.T or mercury porosimetry.

What Number to Use?

  Another known technique is to measure different properties (or sizes) of particles, and we have to use data in many different ways to obtain different average results (D[4,3], D[3,2], etc.). So why should we use number?

  Let’s take spheres with diameters of 1 and 10 units as a simple example. Suppose we are making gold. If we calculate a simple number-averaged diameter, it is given as follows.

 

 

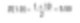
  Thus, we might assume the average size of particles in the system is 5.50 units. However, we must remember that if we are making gold, we should care more about the material’s weight.

  For example, if we want to know the trendiness of the process, we would not be interested in the fact that there are 3.5 million particles there. Instead, our interest would lie in whether we have 1kg or 2kg of gold.

  Remembering that mass average is a cubic function of diameter, we know that a sphere with a 1-unit diameter has a mass of 1 unit, and a sphere with a 10-unit diameter has a mass of 10=1000 units.

  That means the larger sphere makes up 1000/1001 parts of the total mass of the system. If we are making gold, we could discard the sphere that is 1 unit because we would lose less than 0.1% of the system’s total mass. Thus, number average is likely derived from the mass ejected from the system. This is more useful in D[4.3].

  In our example of the two spheres, the mass or volume average moment will be calculated as follows.

 

 

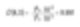
  This figure shows us where the mass lies within the system, which becomes a valuable figure for a chemical process engineer.

  Now, let’s assume we are making silicon or gallium arsenide wafers inside a clean room. Here, if a single particle is placed on the wafer, it tends to create a defect. The number or concentration of particles is highly important in this real-life example because one particle is one defect, leading us to use technology that can directly measure the specific number or concentration of particles. Essentially, this differs from total particle count and particle size. In terms of total count, we record and count each particle. Size is less important, and only a limited scaling amount is needed (as mentioned in 8). From a size perspective, certain sized particles are less relevant compared to their size contributions of their particle bands. Hence, more size bands are required.

  When measuring the inhaler for asthmatics’ one-time portion, both the concentration of the drug and particle size contribution are important.

Mean, Median, Mode – Basic Statistics 

 

Mean

  This is any arithmetic mean of the data. There are many means we can calculate for particles. (Refer to section D[4,3] etc.)

Median

  This is the value of particle size that divides the population exactly into two equal parts. For example, it denotes 50% above and 50% below of the values distribution.

Mode

  The value, such as the highest point of the frequency curve, is the most common value of the frequency distribution. Consider the distribution is Normal or Gaussian. The mean, median, and mode are exactly in the same position. See Fig 4. However, suppose this distribution is bimodal as in view 5.

 

 

  As you can see on the graph, the mean diameter is almost exactly between the two distributions. Mind that such an average-sized particle does not exist. The median diameter is about 1% towards the higher side of the two distributions, because this point exactly splits into two distributions. The mode will be the peak of the higher distribution since it’s the most common value of the diameter.



  This example explains that there is no reason that the arithmetic mean, median, and mode should be ideally or even the same just because of distribution symmetry.