Measurement of Particle Size and Shape through Image Analysis

  Download Materials

What are Particle Size and Shape?

  This material discusses how to calculate the size and shape of particles through image analysis.

What is Particle Size?

  Representing 3D particles is a very complex issue. From a practical view or managerial purpose, it is very convenient to express the particle size as a single number. However, there are many ways to represent the size of a particle when it is not a perfect sphere (which is rare in reality). This is a fundamental challenge in particle size analysis.

  How can we express a 3-D object as a single number? Image analysis captures 2D images of 3D particles and calculates parameters of various sizes and shapes. Calculating diameter includes expressing it as the diameter of a 2D particle with the same area, called the CE diameter (Circle Equivalent diameter). Though different shapes of particles affect the CE diameter, the key point is being able to express it as a single, objective, and reproducible number.

CE Diameter

 The 3D image of the particles is captured in 2D and converted into a 2D circular image with the same area. The diameter of the circle is known as the particle’s CE diameter (See Fig 1).

  Of course, a single value from a single particle is not in high demand, “a single number for managerial purposes.” A single value reliant on individual particles is not statistically meaningful. The number of particles representing the entire sample should be derived through statistical parameters after measurement.

  For instance, something more appropriate that can be expressed as a single specific number is something like the average of all CE diameters. Statistics such as mean, median, mode, standard deviation, D10, D90, etc., are derived from distribution.

  In reality, many samples have the shape of a broad “normal” or “Gaussian” distribution. This allows for identifying accurate parameters and obtaining statistically significant meaning with minimal particle size.

What is Particle Shape and Why is it Important?

 If expressing particle size is complex, determining the shape is even more complex. There are almost infinite ways to express these shapes, and such methods deviate from our fixed purpose of expressing with a single quantitative number. So, why measure shape? Measuring size alone is sometimes not sensitive enough, but there are subtle differences between samples.

  Due to differences between batches, changing to circle equivalent diameter or sphere equivalent diameter makes the differences disappear. For example, consider the three shapes below.

 All three shapes have the same area of 4 squared. If converted to the same diameter, they would all yield a result of 2.257 in diameter.

The downside of measuring only size is that very different shapes of samples can yield the same results because all three shapes have similar 2D projections. Particle shape often significantly impacts quality parameters like flow, abrasion, and bioavailability in final products, making it necessary to differentiate shape.

3 Main Shape Factors – Sphericity, Convexity, Elongation

Sphericity

One method of measurement is how close it is to a perfect circle. Thus, we use a parameter called Circularity defined by the following equation.

  A is the area of the particle, and P is the perimeter.

  Circularity is the ratio between the perimeter of the actual particle shape and a circle with the same area. The given definition includes an area term in both numerator and denominator to detect subtle changes in the relationship between area and perimeter. That is why we use more precise parameters like HS Circularity.

Circularity has a value from 0 to 1. A perfect circle’s circularity is 1, and very jagged or irregular materials are close to 0. Circularity is sensitive to shape and surface roughness. By reviewing the shapes below, one can see how form, symmetry, and surface roughness affect Circularity.

Circularity is an excellent measuring method for determining how far something deviates from a perfect circle. However, it is important to remember that describing a shape with a single parameter does not perfectly depict or represent combined shape properties.

The elongated ellipse at the top right of Fig 3 has the same Circularity as the jagged shape at the bottom left.

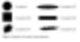
  Thus, parameters have been developed as a suitable toolkit for several shapes. For example, perfectly spherical particles should be measured for QC purposes using Circularity, a parameter capable of distinguishing deviations from a perfect circle. However, Circularity is not suitable for angular or elongated particles.

  Other two parameters used for shape measurement are convexity and elongation.

   Convexity

  Convexity measures the surface roughness of particles and calculates the convex hull perimeter. The easiest way to visualize the convex hull perimeter is to imagine an elastic band around the particle. Convexity also ranges from 0 to 1. Smooth surfaces have a convex hull perimeter of 1 and are equal to the actual parameter. Jagged and irregular particles have a convex hull perimeter close to 0, with the actual value larger due to finely detailed surfaces.

Figure 4 shows that Convexity does not apply to all shapes – the Convexity of the smooth needle shape is the same as that of the smooth circular shape.

   Elongation

Elongation is defined as 1-aspect ratio or 1-width/length. As the name suggests, Elongation measures and ranges from 0 to 1. The Elongation value of symmetric axes, like a circle or square, is 0, and it approaches 0 when the aspect ratio is large. As shown in Fig 5, it is difficult to apply to shapes with surface roughness – the Elongation value of a smooth ellipse is similar to that of a pointed ellipse.

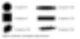
In conclusion, image analysis has two advantages, number-based resolution and storing images. Both provide deeper understanding of products or production processes.

What is ‘Number-Based’ Resolution?

When detecting relatively small particles or unknown samples, the resolution of a number-based system is important. Not all situations require number-based sensitivity. If not needed, it would be because of speed advantages or the convenience of the entire method.

The entire particle size method is known as volume-basis data. This means that particle dispersal is proportional to volume. Larger particles have a significant impact on dispersal, while smaller particles have less impact, being much smaller in volume compared to larger particles.

  Image analysis provides number-basis data. This means that each particle dispersal means that even very small particles have the same size as very large particles.

  If the purpose is diagnostic or troubleshooting, having fine particles is very important, as it provides a deeper understanding of the production process and requires more sensitive image analysis.



Image Recording 

 Visualizing the images of individual particles provides additional insights in quantitative data and sample preparation and method development optimization. Especially with irregularly shaped particles, this ability allows verification of whether they are inherent particles or aggregates. All stored images can be sorted, filtered, and categorized as per users’ needs.

  Fig 7 shows agglomerated spherical particles displayed…”