Rheology Technical Note-Understanding the Correlation between Rheology and Particle Parameters1



Download



Understanding the Correlation between Rheology and Particle Parameters

  The physical properties of particulate materials are affected by both their size distribution and zeta potential (a measure of particle charge), influencing the rheology of the coating materials. The test results addressed various types of coatings under these influences, with rheology measured using a Malvern Bohlin Gemini rheometer. Particle size and zeta potential were measured using a Malvern Mastersizer 2000 and a Malvern Zetasizer Nano ZS, respectively.

  The examples used in this material consider very common conditions in most scenarios, and the theory can be widely applied related to coating systems.

  The “flowability” of a material is represented by its viscosity or resistance to flow. When discussing the viscosity of a specific material, it is crucial to recognize that viscosity represents not just a single value but as a function of shear stress.

  Shear stress provides an indicator of deformation when the material is subjected to small shear stress below 1s-1 or high shear stress above 100s-1.

  Table 1 summarizes the process for coating materials and the resulting shear rate range.

  Considering shear rates, materials used in coating follow the categories below:

– Shear thickening (viscosity increases as shear rate increases)
– Newtonian (constant viscosity across all shear rates)
– Shear thinning (viscosity decreases as shear rate increases)

Relationship between Particle Size and Rheology

  The first consideration is the viscosity of the pressure-sensitive adhesive (PSA: substances that adhere under mild pressure while being tacky even at room temperature). In the case of latex particles, there are two different sizes. As Fig 1 shows, as particle size increases, the viscosity of the PSA noticeably decreases.

  This is solely a result of the change in average particle size. The volume fraction (or the mass of latex added to the PSA) remains fixed. Given the mass of latex, the number of particles will be determined by their size. Hence, there will be more particles of 175 microns size latex than 750 microns size latex.

  This is a general inter-particle reaction, and in bulk materials, there will be fewer interactions, whether it’s mechanical or electrochemical/chemical. Therefore, smaller particles will have more particles present within the same volume fraction, and there will be more interactions.

  When considering interactions in a narrow range of structure, viscosity essentially measures an increase. Shear rate can be considered a deformation factor, and low shear rates will cause smaller deformations compared to higher shear rates. Thus, low shear rate caused by weaker forces and high shear rate caused by stronger forces differ. Fig 1 also shows the greatest viscosity difference at low shear rates because particle interactions are weak and easily breakable.

  Therefore, at high shear rates, these two systems show similar viscosity as particle interaction decreases.

  In the case of resin-based ink (ink using talc as a filler), viscosity within the system will change. This is shown in Fig 2 where the ink mass shows a typical newtonian viscosity. The added resin is a fairly solid material, and the interaction of these polymers indicates very high viscosity due to polymer entanglement resisting shear, shown as the smallest shear thinning.

  For a 19-micron talc particle, large particles have relatively small interactions, indicating an initial rise in viscosity with newtonian characteristics. However, when 5-micron small particles are involved, an increase in high viscosity is observed due to the increased number of particles. Once again, such particle interactions are generally weak. Hence, this shear thinning appears with high viscosity at low shear rates.

Impact of Volume Fraction and Dispersion

  The discussions presented thus far have revolved around a fixed volume fraction of fillers. Essentially, the same particles are distributed into the system. Simply increasing the particle fraction generally suggests a rise in viscosity measured by a viscometer. However, when measuring the rheology in practice, more information is required about the relationship between viscosity and shear rate. Fig 3 shows that ink viscosity increases with higher particle volume fraction across various shear rates. However, flowability also changes.

  At lower volume fractions (below 40%), the particle number in a system remains low enough not to interact significantly, maintaining newtonian characteristics. At around 50%, the number of particles shows an increase in viscosity due to strong interactions. As previously discussed, such interactions are described as weak, resulting in shear thinning effect, breaking these weak structures at high shear rates.

  Systems with high volume fractions over 60% clearly experience more interactions, exhibiting high viscosity at low shear rates and shear thinning behavior. However, the mechanical difficulties of particle movement in such complex systems should be considered. These patterns are notably exhibited at high shear rates and appear as an increase in viscosity, showing shear thickening or dilatant characteristics.

  Viscosity dependent on volume fraction can be expressed by the Krieger-Dougherty equation. η denotes the viscosity of the suspension, and ηmedium represents the viscosity of the pure solvent. φ signifies the volume fraction of solid matter in suspension, and φm indicates the maximum value of this volume fraction.

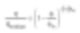
  Additionally, [η] indicates the intrinsic viscosity of the solvent, representing a value of 2.5 in the case of spherical particles. The Krieger-Dougherty equation can vary based on the particle characteristics, even with constant volume fractions. In this instance, it is the particle size distribution or the range of inter-particle distances that directly impact maximum volume fraction (or packing). For a system loaded with single-dispersed spherical particles, the maximum volume fraction is around 64%. However, this too effectively increases with flow around the particles (i.e., when the volume fraction ratio is low). It can be simply thought of as “easy flow” due to decreasing viscosity. Interpreted differently, it indicates that smaller particles effectively serve as lubricants for the movement of larger particles.

  Fig 4 indicates that this exhibits interesting results. It shows that in a polydisperse system made up of large and small particles with fixed solid volume fraction, the viscosity can be lower than each respective viscosity of the large and small particles.

  In coating systems, simply increasing polydispersity or the amount of additives allows for maintaining viscosity under given conditions even after the addition of fillers or pigments.

  The effect of polydispersity should be considered when replacing coating material additives from various suppliers. Since suppliers generally use similar particle sizes, the distribution is unaffected. Therefore, rheological properties remain unchanged. For example, when measuring with a Mastersizer 2000, both particle size and particle size distribution can be measured.