Understanding Laser Particle Size Analyzers and Principles of Particle Size Analysis

Basic Principles of Particle Size Analysis

What is a Particle?

Asking this is a very foolish question. However, in the field of various particle size analysis technologies, this forms the foundation. The dispersion process and the shape of the material become more complex for particle size analysis than initially.

Particle Size Issue

Imagine someone gives you a matchbox and asks you to determine its size. You might tell the person, “Its size is 20*10*5 mm.”
However, saying precisely “20 mm” would be inaccurate, offering only one perspective of its size. Hence, you can’t describe a 3D matchbox with a single unique dimension.

Clearly, the situation is further complicated with irregular shapes like sand particles or pigments in a paint can.  

If I were a Q.A. (Quality Assurance) manager, I would want a single number to describe a particle – for example, whether the average size of the most recent product has increased or decreased. This is a fundamental issue in particle size analysis: how do we express a 3D object with just one number? 

Figure 1 shows some sand particles. What is their size? 

Equivalent Spheres 

There is a sphere that can be expressed in a single unique number. When we refer to a sphere that is 50 μm in size, it is possible to express it accurately…

Many characteristics of a matchbox can be expressed with a single number. For instance, weight related to volume and surface area is a specific number. If we have a technology to measure the weight of a matchbox, we can convert it to the weight of a sphere. 

Remember that the equivalent sphere theory involves calculating a single number, which is the diameter (2r) for a sphere having the same weight as the matchbox. 

We measure a certain property of a particle and assume its shape as a sphere. Therefore, we obtain a single number (diameter of the sphere) to represent the particle. 

This tells us that, when expressing a 3D particle, though it might be inconvenient for more accurate control purposes, there is no need to express it in three or more numbers. 

This illustrates interesting effects depending on the shape of an object, exemplifying a cylinder as shown. (Fig.2)  

However, if the shape or size of the cylinder changes, the volume/weight will change. As an equivalent spherical model, at least we can say it became smaller or bigger.

Equivalent Spherical Diameter of a 100 x 20μm Cylinder 

Assume the cylinder has a diameter of D1=20μm and height 100μm. There’s a sphere with the same volume as the cylinder with a diameter D2. We can calculate the diameter as follows…

The cylindrical volume    

The spherical volume

X is the volume radius value. 

The spherical diameter of a cylinder with 100μm height and 20μm diameter is approximately 40μm. The table below shows the spherical diameters of cylinders of various ratios. The last line indicates a typical flat clay particle, as its height is 20μm with a thickness of 0.2μm, and thus can usually be disregarded in dimension. 

Regarding the instrument measuring particle volume, we may get an answer around 5μm. Therefore, we must employ different techniques to challenge these answers. 

Moreover, each of these cylinders may show similar sizes on a 25μm filter, saying “All items are less than 25μm.” These cylinders could appear differently due to differing values shown in laser diffraction. 

Various Measurement Techniques

Clearly, if one observes a particle through a microscope, a 2D projection will be visible, and there will be measurable particle diameters to characterize the particles. If we adopt the maximum length of the particle and use it as our measure of size, it may suggest that the particle is a globular one with maximum dimensions. 

Similarly, if we use minimum diameter or other measures like Feret’s diameter, it will give us yet another answer on the particle size. Therefore, we must recognize each technique measures different properties of the particle (maximum length, minimum length, volume, surface area, etc.). Hence, measuring selectively may lead to differing results compared to other techniques.

Fig 3 illustrates several different answers that make depicting one grain of sand possible. Each method is not wrong—all techniques are correct, measuring different properties of the particle. It’s like measuring a matchbox by its length versus its width (you may measure the length while I measure the width!). 

Thus, we only have to compare measurements taken using the same technique. It implies that although sand particles don’t have any standard size by themselves, standards should indeed be spherical for comparisons between various techniques. Yet, we can obtain standard particle size by each technique, thus comparing the instruments by the techniques applied. 

D[4,3]

Imagine three spheres with unit diameters of 1, 2, and 3. What would be the average size among the three particles? One might initially say it is 2. How was this answer reached? 
We will add all the values and divide by the total number of particles.

This is the number average (more precisely, the length-based number average). The number of particles can be expressed in equations. 

Mathematically, it is referred to as D[1,0] since the diameter term in the equation above is raised (d1) and the denominator has no diameter term (d0). However, if I’m a chemical engineer, I might want to compare these spheres based on surface area because higher surface areas lead to higher catalytic activity. 

The surface area of a sphere is . Therefore, when making comparisons based on surface area, we should first determine the square of the diameters divided by the number of particles, then take the square root to return to the average diameter. 

Again, this is an average number (surface-average number), the reason being that the number of particles appears in the equation below. We sum the squares of the diameters, and therefore mathematically it is called D[2,0] – the equation’s top term is squared while the bottom has the diameter term. If I were a chemist, I would be interested in comparing by fundamental sphere weight, and the formula for sphere weight is as follows… 

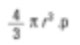
We then total the cubes of squares divided by the number of entities before taking the cubic root to return to the average diameter.