Optimizing powder packing behavior by controlling particle size and shape

The manufacture and use of cement is interesting, combining the unit operations of comminution and agglomeration not once but twice. Blocks of limestone are hewn from the earth and crushed and ground before being combined in a rotary kiln to produce balls of clinker. This clinker is then ground again, other materials added (such as gypsum) and powdered cement is the outcome. We use that powdered cement in order to make larger blocks of material…. Why didn’t we use the blocks of limestone in the first place? Well, in many cases we do. The Great Pyramid in Giza is made out of limestone blocks, as are many of the buildings in Kingston, Ontario (Canada) which is dubbed ‘Limestone City’. However, it is the convenience of powder processing and handling, as well as the ability to form complex shapes, colors and enhanced structures, by what is effectively an additive manufacturing process, that makes cement and concrete so much more useful and versatile.

There are drawbacks to powder processing though – particle size and shape distributions are key to producing a robust finished article, which could be a block of cement or a plate or cup in the porcelain ceramics field. For these applications the presence of particle agglomerates can be problematic since they tend to produce voids in the structure which are the source of weak points from which crack propagation can commence (Griffith 1921).

The Griffith equation (incidentally “The proof is due to Mr C Wigley” is present in a footnote in the original paper) is important in explaining the fracture mechanics of such systems and show that materials fail long before their tensile strength would predict due to the presence of microscopic flaws similar to that illustrated in Figure 1. This can be explained by thermodynamic consideration of the stress required to form new surface:

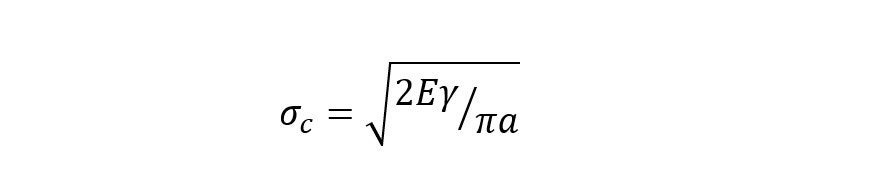
where σ c is the critical stress required for fracture, E is Young’s Modulus, γ is the surface energy density and 2a is the crack length.

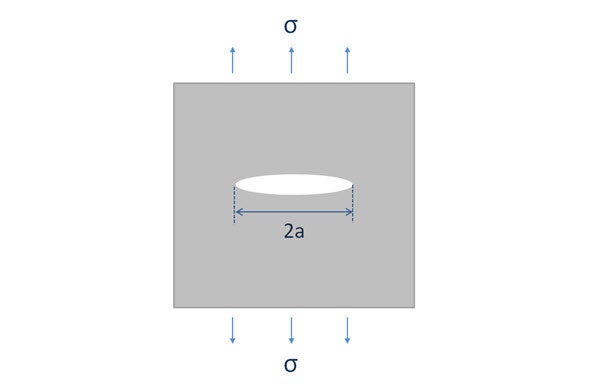
Figure 1 - Illustration showing a thickness of sample with a lens shaped crack of length 2a subjected to a tensile stress

We also have the fundamental issue that powders constituted of small primary size particles ( c ) below which fracture is considered impossible under compressive forces.

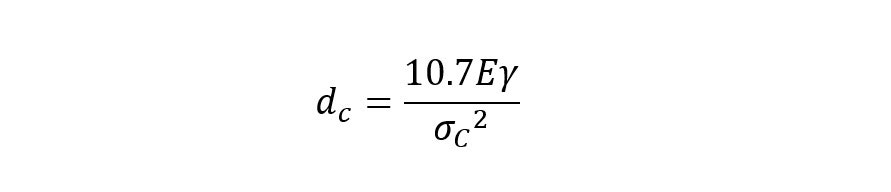
For a sample of calcite where E ≈ 72 GPa, γ ≈ 0.347 Jm -2 and σ c ≈ 100 MPa the calculated value for d c is approximately 1 μm.

In researching high performance materials, the goal is often to produce an article of high strength and, in general terms, this comes from a material exhibiting the following properties:

Low molecular mass High melting and boiling points High density High Young’s modulus There is shape dependence to strength also, with whiskers of material possessing more flexural strength than platelets or crystals. Thus, we see the importance of carbon fiber and carbon nanotubes. There is then the challenge of constructing these with as small a primary size as possible but not too small. The Hall-Petch conjecture (Hall 1951, Petch 1953) explains that we can increase strength by decreasing the primary grain size but lower than a limiting size the dimensions of dislocations begin to approach the size of the grains. At a grain size of around 10 nm perhaps only one or two dislocations can fit inside the grain. From an applications perspective we can look at both the material itself and also the spaces in between. A whole bunch of properties relate to optimum packing of particles. We have (among others):

Final strength – best if the aggregates and agglomerates are minimized and the primary size is as small as possible Rheological and flow properties (both in the slurry and dry states) - non-optimal grain flow in silos is literally a life and death issue with many farmers dying each year from silo accidents Porosity/pore size distribution - important for applications ranging from catalysis to water flow through soils Packing potential/packing density – get this right and the strength of the final structure is maximized Drying and firing shrinkages – in the ceramic sand and powder metallurgy industries these can be the cause of product failure Surface area – often it is desirable to maximize this. It’s not simply a size reduction issue but optimal surface area needs to be balanced against undesired aggregation at really small primary particle sizes or environmental hazards such as dusting tendency The understanding of particle packing has occupied theorists since the 1500’s (stacking of cannonballs on a ship deck) and we need to look at the problem in stages. It’s obvious with hindsight that some shapes can be packed in 3-dimensions with no void space whatsoever – cubes, cards, bricks. There are more trivial (but tougher to solve) examples such as packing your suitcase with souvenirs or getting your fishing tackle into the trunk of your car. From an economic perspective, aircraft or ships holds that are only partially full may cost the owners money and one practical international solution has been the standardization of containers and pallets to allow these to fit or stack neatly next to each other in 3-dimensions. As you might surmise there are global (ISO 668) standard ocean freight containers .

In 2-dimensions there are some interesting packing geometries (e.g. Penrose tiling, the mathematical art of M C Escher ) and in 3-dimensions space we can have quasi-crystals, but it’s really quite difficult to visualize 3-D packing so we have to take this gradually in stages to gain more insight.

Close packing of monodisperse spheres: This has implications in crystallography and interestingly represents the shape where it’s possible to have the greatest free space in a packed system. From a theoretical perspective, it’s the most studied situation but we still have to distinguish 2-D (circles, disks) from 3-D (spheres) as often the former is used to diagrammatically represent the structure. Here we can have the densest packed structures with what is termed hexagonal close packing (HCP) and face centered cubic structures (FCC) in both of which a central sphere touches 6 other spheres in the same plane and 12 contacts in total giving a maximum packing fraction of 74% – that is 26% void space.

Random packing of monodisperse spheres: This seems a strange concept but is the practical situation from loose assemblages. For example, this is the real world situation of pouring marbles or ball bearings into a box or jar. This has also been extensively studied and gives rise to what is termed Bernal packing where we can achieve 64% packing (and thus 36% void space) for a sample of relatively monodisperse spheres.

Random packing of polydisperse spheres: In this case we can start to ‘fill in the gaps’ between the spheres and mixes of 2, 3 and 4 different sizes have been dealt with on a theoretical basis. This is the basis of Apollonian packing and has even been studied in multi-dimensions. A practical application is in the production of oil-in-water emulsions where a mix of sizes can significantly increase the loading of the oil phase without any increase in viscosity. Bimodal systems were obviously first studied and a large viscosity reduction can be attained by tailoring the drop size distribution, so that the coarse emulsion has a very narrow size distribution mixed with a finer polydisperse system. The general shape of the plot (maximum in the packing fraction for an optimum composition) for bimodal mixtures is shown in various articles. For example, Kyrylyuk has published extensively in this area.

Random packing of monodisperse non-spherical/irregular particles: This may be the packing of identical pasta shapes or electrical plugs in a box. This problem is close to being insoluble although computing power has advanced such that programs (e.g. DigiPac) are available that will demonstrate packing and flow of the aforementioned objects. There just appears to be no universal and applicable solutions in this area.

Random packing of polydisperse non-spherical/irregular particles: Imagine toy soldiers in a box… In fact, this was the earliest type of real world system studied and reported in the paper of Furnas (1931) on grading aggregates. This showed for 2, 3, and 4 component systems that the densest packing approached 97% for all systems. The key parameter here is the ratio between the particles of largest and smallest sizes and the higher this ratio then the better achievable packing.

Ratio of particle diameter(s) of the size fractions Ratio of fractions (wt%) Maximum packing density (vol%) d 1 100 64 d 1, 1/7d 1 84/15 86 d 1 , 1/7d 1 , 1/49d 1 75/14/11 95 d 1 , 1/7d 1 , 1/49d 1 , 1/343d 1 72/14/10/3 98 Table 1: Effect of particle size distribution on maximum packing density of randomnly dispersed spheres (A V Shenoy “Rheology of Filled Polymer Systems” Springer page 268 (1999))

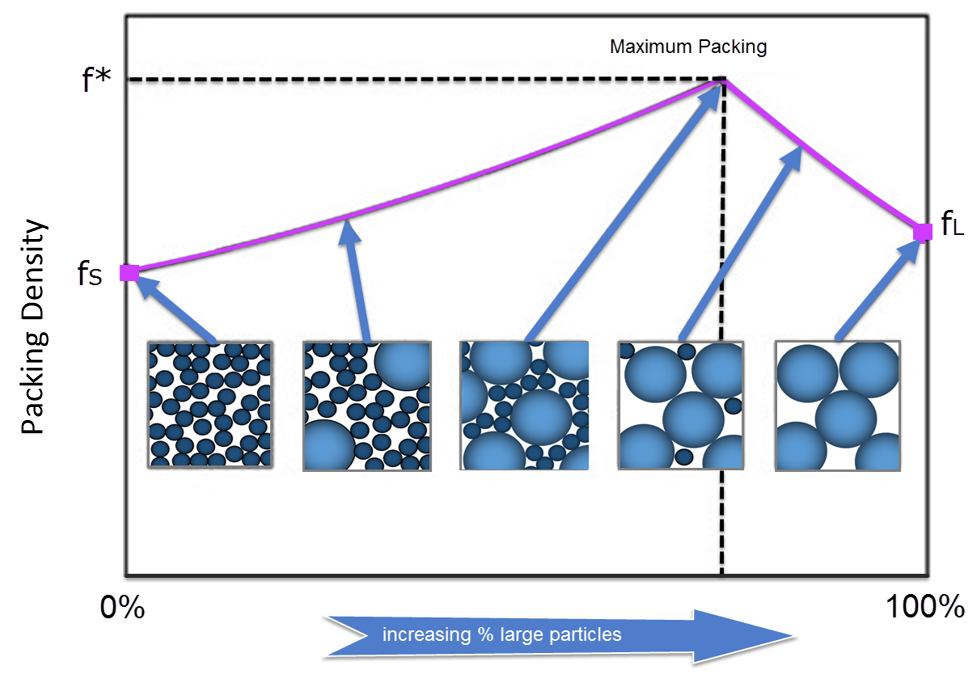
Figure 2: Packing density (f) for a bimodal particle mixture of small and large particles (Fundamentals of Refractory Technology; James P. Bennett & Jeffery D. Smith, Ceramic Transactions, Volume 25, 2001 (American Chemical Society)

From a practical perspective, Dinger shows optimum size distributions for a continuous distribution of particle sizes by employing the Dinger-Funk equation below.

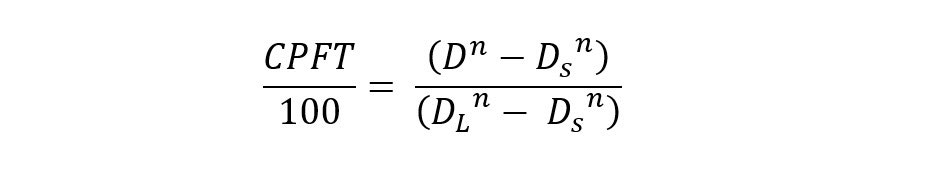
Where, CPFT is the cumulative (volume) percent finer than, D is the particle size , D S the minimum particle size and D L the largest particle size. The exponent n is a distribution coefficient and gives an indication of the amount of fines and coarse material that can be accommodated.

The densest packing is obtained with the so-called 'Fuller’ distribution. This theoretical distribution consists of several monosized particle fractions, the sizes and amounts of which are just sufficient to fill the voids developing between particles of the next larger fraction. So-called Apollonian packing (hexagonal) of spherical particles is one example. In terms of irregular shapes then theoretical mixes of spheres and rods have been studied by the earlier mentioned Kyrylyuk (2001). Even in the road construction industry there are practical applications where the same previously optimum maximum is shown for coarse and fine aggregates reminiscent of the early work of Furnas (1931).

So, in conclusion, we see the combination of theory for known shapes (invariably spherical) and sizes (mono and polydisperse) directed toward the practical applications for mixes of shapes and sizes. Perhaps we can use a quotation from USP the pharmaceutical standard for optical microscopy: “For irregularly shaped particles, characterization of particle size must include information on particle shape”.

References T Aste, D Weaire “The Pursuit of Perfect Packing” Institute of Physics Publishing (2000)

AA Griffith 'The phenomena of rupture and flow in solids' Philosophical Transactions of the Royal Society of London, A, 221 pp 163–198 (1921)

MN Rahaman “Ceramic Processing and Sintering” CRC Press (2003)

K. Kendall 'The impossibility of comminuting small particles by compression' Nature, 272, pp. 710–711 (1978)

EO Hall 'The Deformation and Ageing of Mild Steel: III Discussion of Results'. Proc. Phys. Soc. London. 64 747–753 (1951)

NJ Petch 'The Cleavage Strength of Polycrystals'. J. Iron Steel Inst. London. 173 25–28 (1953)

D R Dinger “Particle calculations for ceramists” Dinger Ceramic Consulting Services (2001)

AV Kyrylyuk, AP Philipse “Effect of particle shape on the random packing density of amorphous solids” Phys. Status Solidi A 208, No. 10 2299–2302 (2011)

Eds. R A Terpstra, P P A C Pex, A H De Vries “Ceramic Processing” Chapman and Hall (1995)

W A Gray “The packing of solid particles” Chapman and Hall (1968)

G G Szpiro “Kepler’s Conjecture” John Wiley & Sons, Hoboken, New Jersey (2003)

Webinar: October 21st, 2015 ' In pursuit of perfect packing '

Optimizing powder packing behavior by controlling particle size and shape

Login

Popular links

Support and services

Company profile

Legal information