X-ray powder diffraction (XRPD) has been a powerful tool for metallurgy for over 100 years [1, 2]. Despite the misleading name, X-ray powder diffraction is used for analysis of more than just powder- it is routinely used for the non-destructive analysis of metal sheet, wire, and parts. XRPD is a well-established method for production control using phase identification, phase quantification (such as retained Austenite), texture and residual stress analysis of manufactured parts. Given its credentials as an established non-destructive characterization method, XRPD should be a powerful solution for process development and optimization, non-destructive validation of parts, and certification of production machines that is needed for the widespread commercialization of additive manufacturing [3]. XRPD has been used for research studies for analysis of additively manufactured parts, primarily for phase identification during alloy development and residual stress analysis [4, 5, 10]. However, it is not universally used in process studies or commercialization strategies because additive manufacturing can routinely produce parts with grain sizes 100 µm and larger [6]. The ideal specimen for XRPD analysis has a crystallite size less than 1 µm. In this whitepaper, we discuss the challenge of grain size for XRPD analysis of additively manufactured parts, and strategies for overcoming these challenges.
X-ray powder diffraction (XRPD) is a nondestructive analytical technique used to identify and quantify phases in a material. The term “phase” refers to a material with a distinct atomic structure, determined by what atoms are in the phase and how they are arranged. Every crystalline phase produces a characteristic diffraction pattern (e.g. fingerprint), even phases that are chemically identical. Figure 1 shows the atomic structures and diffraction patterns for different phases of steel. A pure material will show one of these diffraction patterns while a mixture of the three phases will show characteristics of all three diffractograms with peak height indicative of the relative concentrations.
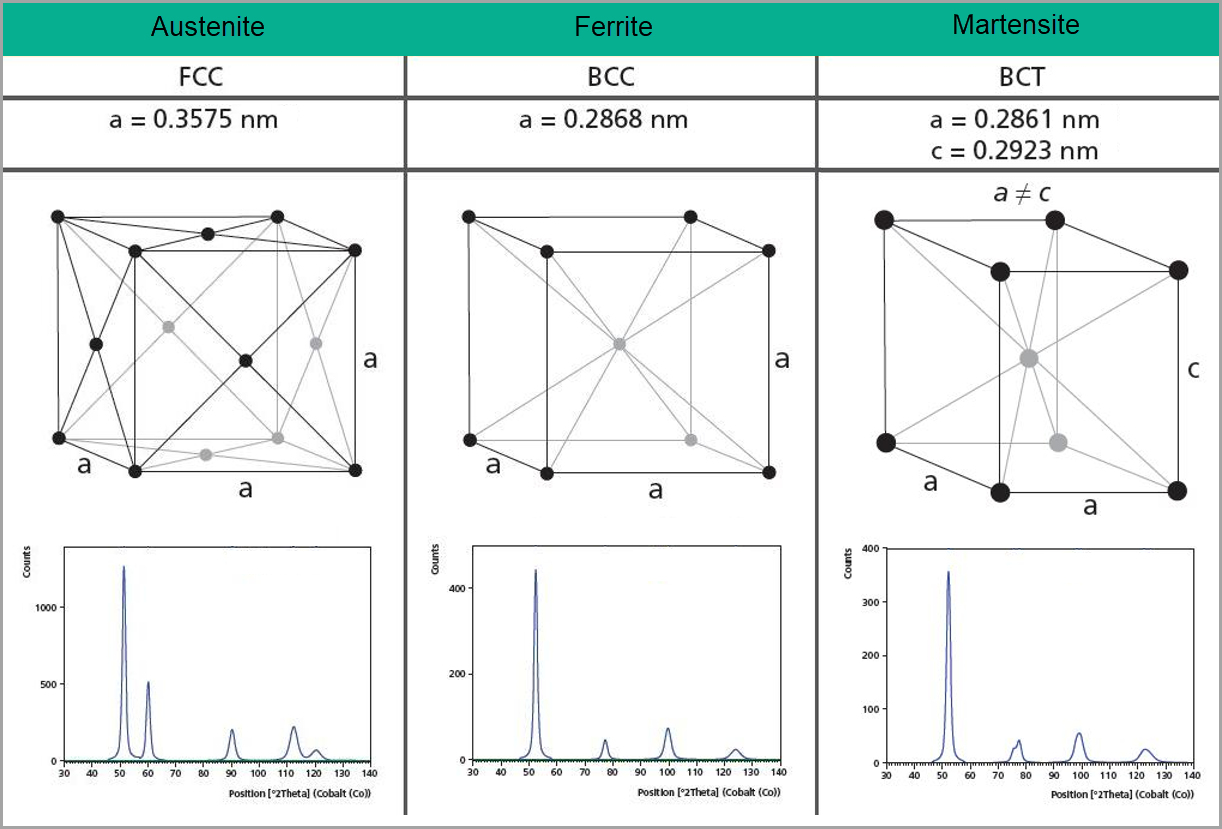
Figure 1. Illustrations of the crystal structures of Austenite, Ferrite and Martensite and their corresponding diffraction patterns.
The characteristic diffraction pattern is created when incident X-rays are scattered by the orderly three-dimensional arrangement of atoms in a crystal, producing an interference effect that constructively reinforces the X-ray beam at specific directions and results in a diffraction peak, as illustrated in Figure 2. The diffraction peak is produced based on the interatomic spacing, as defined by Bragg’s law. It is these reinforced diffracted X-rays that produce the characteristic X-ray diffraction pattern that is used for crystal structure determination.
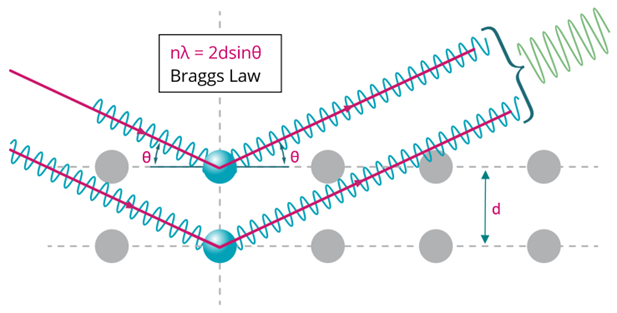
Figure 2. Illustration of Bragg diffraction in which two beams with identical wavelength and phase are scattered off two atoms with spacing d to give constructive interference.
In addition to phase analysis, X-ray diffraction can be used to analyze several microstructural features that will affect the diffraction pattern. Texture creates variations in peak intensity; residual stress creates variation in peak position; and crystalline size and defect concentration creates variations in peak width.
Before diving into a discussion about the problem of grain or crystallite size in X-ray powder diffraction, it is helpful to define what these terms mean in the context of the technique. A crystallite is defined as a unit volume where the atomic structure is undistorted, producing continuous crystallographic planes with uniform lattice spacing. Anything that disrupts the uniform lattice spacing and orientation will form a boundary for the crystallite. This may be a grain or particle boundary, but may also be a dislocation wall, antiphase domain boundary, or similar distortion of the atomic structure. A grain is a unit volume where the crystallographic planes are generally parallel. A grain boundary is created by a change in the direction of the crystallographic planes that maintains some atomic bonding across the grain boundary. A particle is a discrete unit volume that does not share atomic bonding across the boundary with neighboring particles. As such, a particle may contain multiple grains, and a grain may contain multiple crystallites. Techniques such as EBSD will measure grain size while for XRPD the measured domain is a crystallite, though in some cases they may be one or the same.'
The problem of large grain sizes is well-known in XRPD analysis. It is often called “particle statistics” [7], though the term “crystallite statistics” is more accurate as these are the diffracting domains in an XRPD experiment [8]. X-ray powder diffraction assumes that a statistically enough crystallites are irradiated by the X-ray beam to produce an accurate measurement of diffracted intensity, and a smooth diffraction peak that can be fit and analyzed by software. Achieving adequate crystallite statistics is difficult because only a small fraction of crystallites in a specimen will be properly oriented to diffract. For example, a sample with 1 µm average crystallite size will have 38,200,000,000 crystallites within the irradiated volume; but only 38,000 (i.e., 0.0001%) of the crystallites will be properly oriented to diffract at any given Bragg angle [8].
Poor crystallite statistics will affect the precision and accuracy of intensity measurements, the precision of peak position measurements, and the precision of peak width measurements. Figure 3 shows the standard error in intensity calculated as a function of crystallite size for diffractometers with differing goniometer radii (i.e., the distance from the source-to-sample and the distance from sample-to-detector).
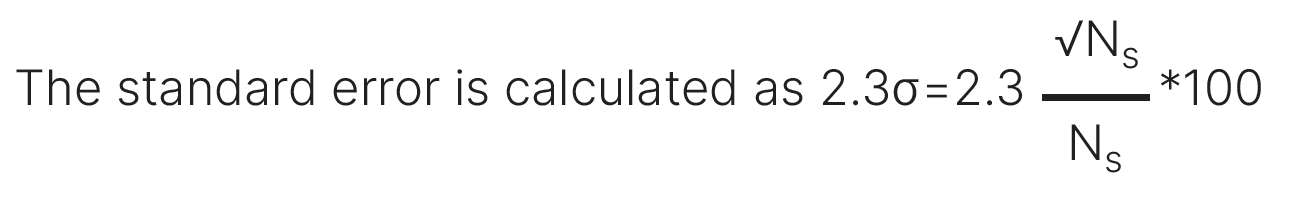
where Ns is the number of diffracting crystallites for a given diffraction peak [8]. The fraction of crystallites contributing to the measured intensity, Ns, is calculated using equations derived by Jenkins and Snyder [15]. Ns depends on goniometer radius, the take-off angle of the incident X-rays, and the size of the receiving slit aperture, as well as other factors.
As shown in Figure 3, even a specimen with 1 µm crystallite size will produce >1% standard error. As calculated by Davis et al [8], there should be approx. 53,000 diffracting crystallites in a specimen to produce standard error less than 1% for the intensity of a given diffraction peak. A specimen with a 1 µm crystallite size will contain only 38,000 diffracting crystallites in the standard irradiated volume. This is still much better than a specimen with a 40 µm crystallite size, which will contain only 12 diffracting crystallites and can produce a >100% standard error in the measured peak intensity.
Figure 3 not only illustrates that standard error increases quickly with crystallite size, but that a longer goniometer radius also increases the standard error in measuring peak intensity. While a shorter radius will improve crystallite statistics, it must be balanced against the optics and detector to maintain suitable angular resolution at that radius.
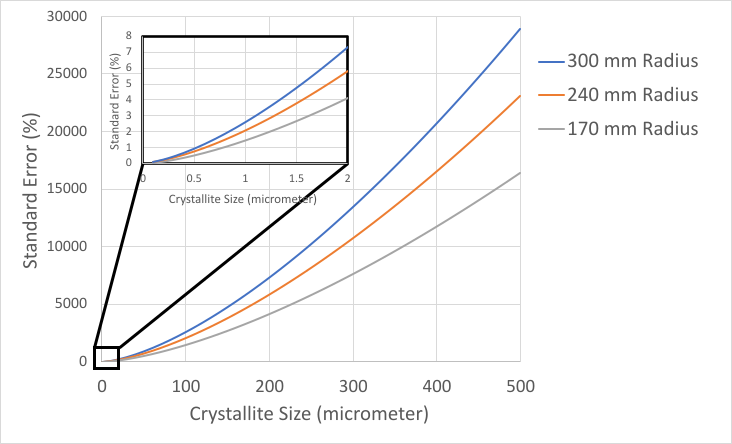
Figure 3. Standard Error as a function of crystallite size calculated for instruments with different goniometer radii.
Poor crystallite statistics can also produce inaccurate peak intensity measurements because XRPD assumes that every diffraction peak is the product of diffraction from a statistically equivalent number of crystallites. This assumption is not valid in a specimen with poor crystallite statistics [11, 12]. Consequently, any analysis that relies on accurate peak intensities—such as phase quantification and texture analysis— will fail.
The above numbers are calculated for a 20 mm3 irradiated volume that is produced by a conventional powder diffractometer using a ½ deg fixed divergence slit and 13 mm beam width to analyze a SiO2 material. It has become popular to analyze manufactured parts with microfocus sources that produce ≤0.4 mm diameter X-ray beam. While these sources provide improved spatial resolution, the number of irradiated grains is significantly diminished. The crystallite statistics can be improved by combining a large area detector with the microfocus source, which increases the fraction of the Debye diffraction ring observed, effectively increasing the receiving slit aperture [9]. However, when the grain size is 40 µm the maximum number of crystallites irradiated is still limited to approx. 375, which will not produce sufficient crystallite statistics for accurate analysis.
The effect of poor crystallite statistics on peak intensity is well-documented [11, 12]. Less well-documented is how poor crystallite statistics also compromise the accuracy of peak position measurements, which will produce errors in lattice parameter and residual stress calculations. This problem is illustrated in Figure 4, which compares the 2D and 1D diffraction patterns of SiO2 specimens with 8 and 27 µm average crystallite size. The 2D diffraction pattern shows a segment of the Debye diffraction ring. The ideal powder specimen produces a Debye diffraction ring that appears as an arc of continuous and even intensity. The 2D diffraction pattern from a specimen with large crystallite size shows individual diffraction spots, rather than an arc of intensity. Each spot in the 2D diffraction pattern essentially represents diffraction from a crystallite. The 2D diffraction pattern can be converted into an equivalent 1D diffraction pattern by integrating the data in arcs corresponding to Debye rings.
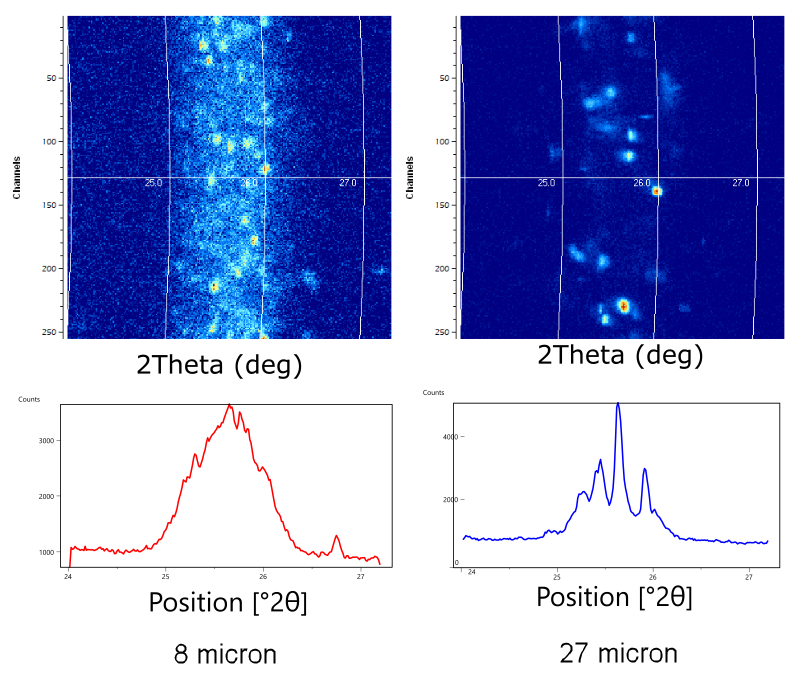
Figure 4. Comparison of 2D XRPD diffraction patterns (top) between sand specimens with 8 and 27 µm crystallite size. The 1D XRPD patterns (bottom) were produced from the 2D diffraction patterns by integrating the intensity along arcs in 0.02 deg increments.
Even though the spots seen in the diffraction rings in Figure 2 are all produced by diffraction from a single Bragg angle, the diffraction spots appear to be distributed across a range of 2theta values. This occurs because the X-ray beam footprint has a finite length on the sample. This footprint is imaged by the position sensitive detector, as illustrated in Figure 5. Crystallites in different positions of the footprint will appear to diffract at different 2theta values. The divergence of the incident X-ray beam will also contribute to the peak width and may be affected by the distribution of diffracting crystallites at different rocking angles within the irradiated volume. This effect can be reduced by using a smaller incident X-ray beam, which will adversely affect the crystallite statistics. It can also be reduced by using a parallel-plate collimator with small angular aperture.
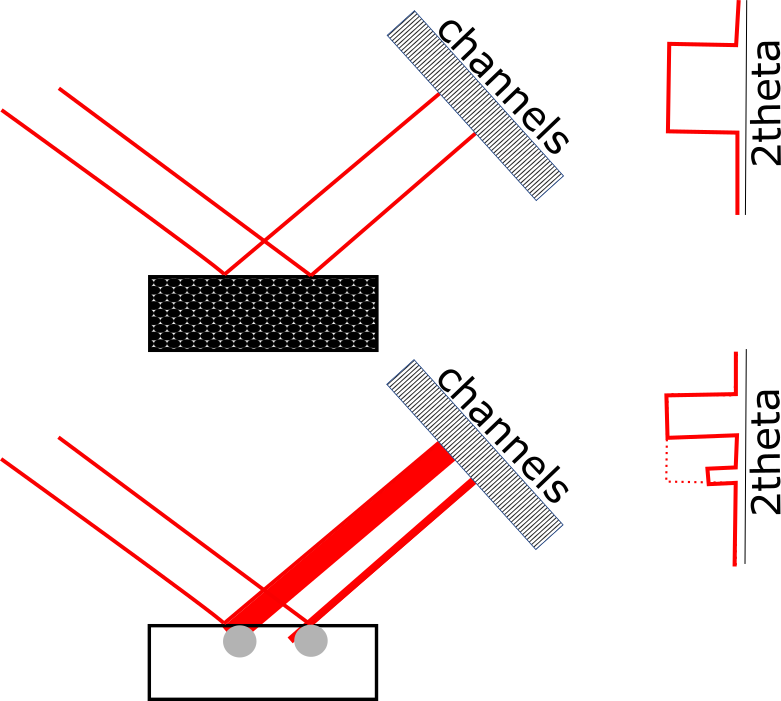
Figure 5. Illustration of how the distribution of diffracting crystallites create the appearance of diffraction peaks at different 2theta values. The different channels in the detector are each assigned a different 2theta value during a measurement.
Crystallites diffracting at the same Bragg angle but from different positions in the beam footprint will be detected at different channels, which will be converted into a range of 2theta values. When the crystallite size is small, the distribution of intensity across the detector channels will be uniform and observed as a single broadened peak (top illustration); when the crystallite size is large, only a portion of the beam footprint will be diffracted, and this will appear as separate peaks on the detector (bottom illustration).
The specimen with 8 µm crystallite size produces a diffraction ring of overlapping spots in the 2D diffraction pattern. When the 2D pattern is integrated into an equivalent 1D diffraction pattern, it produces a diffraction peak with a standard and easily characterized shape. The spread of the intensity distribution across a 2theta range is well-understood and readily modeled with profile fitting software [13], allowing the peak position to be accurately determined to be 25.67 deg 2theta. In contrast, the specimen with 27 µm crystallite size produces discrete diffraction spots spread over a 2theta range. Each different crystallite within the beam footprint and with a different orientation produces a spot at a slightly different angle because of the divergence of the X-ray beam. When this “spotty” diffraction pattern is converted into an equivalent 1D pattern, a series of sharp spikes of intensity is produced. It is impossible to calculate an accurate diffraction peak position from these data.
Despite the challenges of crystallite statistics, XRPD has been successfully used as a research tool for analysis of additively manufactured (AM) parts, such as the determination of γ’ and γ’’ precipitates in Inconel 718 [4, 5]. In a previous study [10], XRPD was used to study the variation of phase composition in feed powder and parts as excess powder was recovered and recycled into the powder hopper between successive builds. As shown in Figure 6, XRPD was able to clearly distinguish the diffraction peaks of the face-centered cubic (FCC) Inconel 718 gamma phase and the body-centered tetragonal (BCT) γ’’ phase. While XRF analysis indicated that chemical composition did not vary, quantitative XRPD analysis revealed that parts had significantly more γ’’ phase than the powder; and that the phase composition of both the recovered powder and parts varied slightly between builds. This study was successful partially because the grain size of the Inconel 718 was sufficiently small to provide adequate particle statistics.
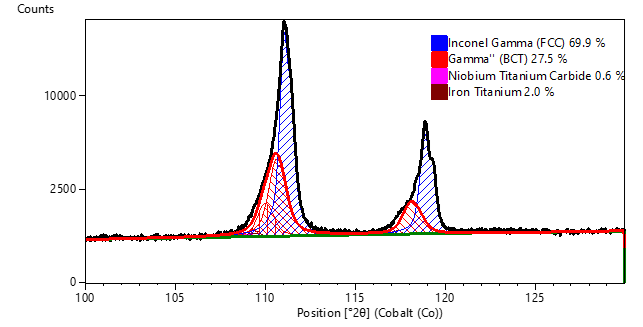
Figure 6. The measured diffraction data (black) from as-received powder was modeled as a combination of the diffraction profiles of γ (blue) and γ''(red) diffraction peaks. Trace amounts of (Nb,Ti) C and Fe2Ti were quantified based on diffraction peaks observed in the 40 to 60 deg 2theta range (not pictured in this figure).
Traditional methods to improve crystallite statistics of a powder sample include grinding the specimen to a small particle size, sieving the sample with 325 or better mesh, and repacking and remeasuring the powder specimen multiple times [11]. None of these techniques are suitable for AM parts. Spinning or oscillating the specimen during data collection can also improve crystallite statistics, but this is not suitable for many AM parts that are large or have complex shapes.
Other conventional techniques, available on most diffractometer platforms, that can be successful in improving particles statistics include:
To demonstrate the effectiveness and limitations of these approaches, XRPD data were collected from coupons of Fe- 3wt% Si soft magnetic steel built using laser powder bed fusion. Details of the scan strategies and microstructure analysis were published by Haines et al [14]. XRPD data were collected using a Malvern Panalytical Empyrean diffractometer with Co anode X-ray tube, Bragg-Brentano HD incident-beam optic, and GaliPIX detector. Figure 7 compares the diffraction patterns of Fe-3wt% Si specimens printed with the longitudinal raster scan strategy as-fabricated, annealed in flowing argon at 1000°C for 5 minutes and for 1 hour, and annealed in H2 at 1000°C for 4 hours. The as-fabricated sample shows a single diffraction peak, consistent with ferritic BCC phase. Note that, as with most powder diffractometers, each diffraction peak consists of a peak doublet due to the presence of characteristic K-alpha1 and K-alpha2 wavelength X-rays. The samples annealed in Argon show two diffraction peaks, indicating phase separation or another effect.
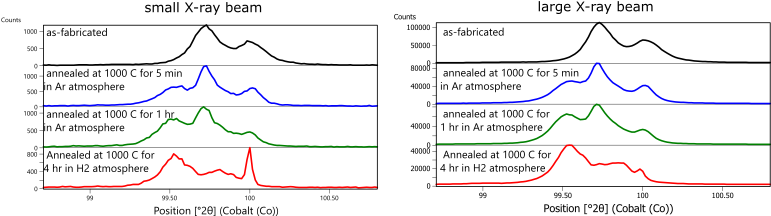
Figure 7. XRPD data collected from Fe-3wt% Si using a small X-ray beam, ie 1/16 deg divergence slit and 0.5 mm x 9 mm footprint (left) and a large X-ray beam, i.e., ½ deg divergence slit and 4.5 x 27 mm footprint (right). The most significant difference between data collected with the two different configurations is the improved peak shape when using a larger X-ray beam to measure the specimen annealed at 1000ºC for 4 hours in H2.
All samples have a grain size that is larger than as measured using EBSD. The as-fabricated sample has approx. 100 µm average grain size, the samples annealed in Argon have approx. 200 µm average grain size, and the sample annealed in H2 has a >500 µm average grain size. These data were collected using two different X-ray beam sizes: a small beam utilizing 1/16 deg divergence slit and 2mm mask, which produces an irradiated footprint of 0.5 mm x 9 mm; and a large beam using a ½ deg divergence slit and 20 mm mask that produces an irradiated footprint of 4.5 x 27 mm. Data from both configurations were collected with the detector in stationary mode. The benefits of the larger X-ray beam can be quantified when the diffraction data are profile fit using a pseudo-Voigt peak shape. Table 1 compares several parameters that evaluate the goodness of the fit, such as the weight residual of the fit and the estimated standard deviation (ESD) of the peak position and intensity. While these parameters do not provide the true precision of the measurement, they are a useful tool for evaluating how will the diffraction data conform to the standard peak models. Data collected with the larger X-ray beam consistently provide better residuals and ESD’s.
| As fabricated | Annealed for 5 min in Ar | Annealed for 1 hr in Ar | Annealed for 4 hr in H2 | ||
|---|---|---|---|---|---|
| wRp (%) | Small beam | 7.5 | 4.7 | 9.0 | NA |
| Large beam | 5.1 | 2.1 | 3.3 | 6.5 | |
| ESD of Peak Position | Small beam | 0.00002 | 0.00002 | 0.00004 | NA |
| Large beam | 0.0000004 | 0.0000007 | 0.0000009 | 0.000001 | |
| ESD of Peak Area | Small beam | 0.05 | 0.2 | 0.2 | NA |
| Large beam | 0.05 | 0.2 | 0.2 | 0.2 | |
| ESD of Peak Width | Small beam | 0.00007 | 0.00007 | 0.00009 | NA |
| Large beam | 0.000001 | 0.000002 | 0.000002 | 0.00003 | |
Table 1. Goodness of Fit parameters that can be used to evaluate how well the measured diffraction data conform to peak shapes that can be modeled and fit using standard profile fit functions. For all parameters, a smaller value represents a better fit and more precise analysis.
The improvement is most readily noticeable in data from the specimen annealed in H2. When analyzed with a small X-ray beam, the diffraction data exhibits the “spotty” peak error associated with poor crystallite statistics. This error makes it difficult, possibly impossible, to accurately analyze the data. When the same specimen is measured using the large X-ray beam, the diffraction peaks are still non-ideal but can now be fit and semi-quantitatively analyzed.
The larger X-ray beam improves the crystallite statistics and resulting data; but a larger X-ray beam is not always a viable solution, especially when analysis requires spatial resolution of regions of interest. In cases where the X-ray beam must be smaller, then a scanning detector mode can also be used to improve the crystallite statistics.
When a linear (1D) or area (2D) position sensitive detector is used in scanning mode, then the effective crystallite rocking angle is increased, substantially increasing the number of crystallites contributing to the diffraction peak. This is effectively using the rocking (i.e., wobble) strategy recommended by Davis et al [8].
Figure 8 compares the static and scanning 2D diffraction measurements of the (110) peak, and integrated 1D scans, for Fe-3wt% Si produced using the rotated raster direction and then annealed at 1000°C for 1 hour in H2. In the static 2D measurement, the diffraction pattern is dominated by a single diffraction spot at 52.4 deg 2theta; whereas in the scanning 2D measurement the diffraction intensity is distributed amongst many spots more closely approaching an ideal diffraction ring. This is highlighted in the integrated intensity vs gamma plot, which shows how intensity is distributed along the arc of the Debye diffraction ring. In the static measurement, a peak at -3 deg gamma dominates the plot. In the scanning measurement, intensity is broadly distributed across the full observed gamma range. The scanning measurement does not match an ideal powder specimen, which would have a smooth and constant intensity at all gamma values; but the scanning measurement clearly represents data more closely approaching ideal crystallite statistics.
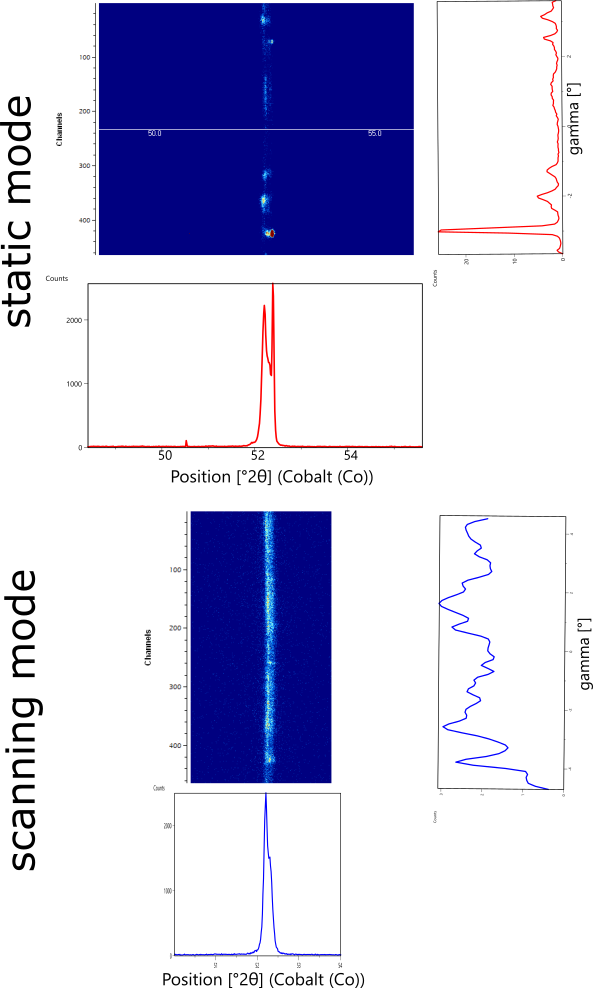
Figure 8. Comparison of data collected using static (top) and scanning (bottom) 2D detector to measure Fe-3wt% Si annealed at 1000ºC in H2 for 4 hours, which has average grain size >500 µm. 1D plots show intensity integration along 2theta and gamma directions.
When a large X-ray beam and scanning mode data collection are combined, the crystallite statistics can be considerably improved. Figure 9 compares data all longitudinal specimens using a scanning 1D mode with a large X-ray beam using ½ deg divergence slit and 20 mm mask that produces an irradiated footprint of 4.5 x 27 mm when measuring the (211) peak at 99.5 deg 2theta. The scanning 1D mode discards some of the microstructural information that can be derived from a 2D scan, but the scanning 1D mode allows a much larger X-ray beam to be used.
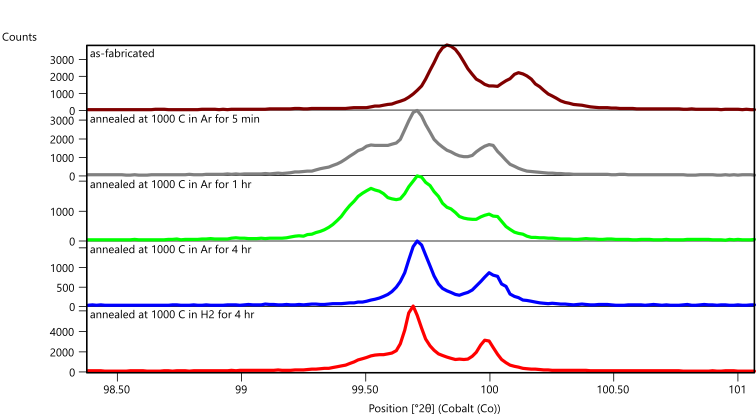
Figure 9. Diffraction data collected in scanning 1D mode from Fe-3wt% Si printed using the longitudinal raster pattern, as fabricated, as annealed at 1000°C in flowing Ar for 5 minutes, 1 hour and 4 hours; and annealed at 1000°C in flowing H2 for 4 hours.
The as-fabricated specimen is purely BCC Fe, as indicated by the single (211) diffraction peak at 99.8 deg 2theta, while the annealed samples contain varying amounts of a secondary phase indicated by a diffraction peak at 99.5 deg 2theta. Phase analysis and whole pattern fitting was performed on data from the as-fabricated sample and from the specimen annealed in Argon for 1 hour, which exhibited the strongest peaks of the secondary phase. This specimen was also the only one to exhibit a third phase, as shown in Figure 8.
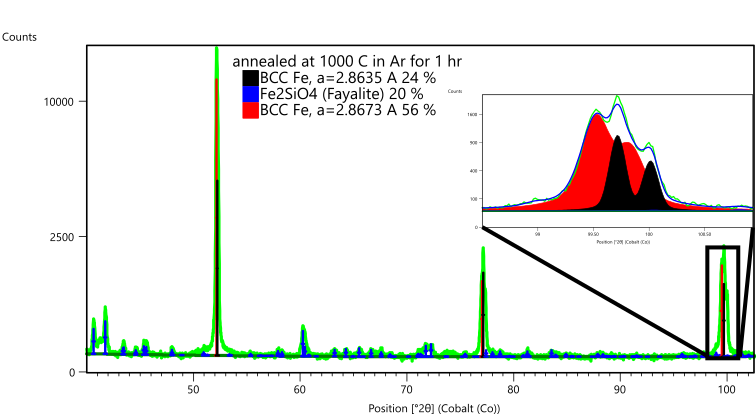
Figure 10. Phase analysis of specimen Fe-3wt% Si annealed at 1000ºC in Ar for 1 hr. The inset shows a section of the whole pattern fitting used to quantify the Fe-based phases in the specimen.
Whole pattern fitting of data from the as-fabricated specimen indicates a BCC Fe phase with lattice parameter a= 2.8633 A. This lattice parameter is consistent with reported values Si-doped Fe [16], which is slightly smaller than pure Fe. The fitting also indicated a slight <001> texture.
The specimen annealed at 1000°C in Argon for 1 hour contained two BCC Fe phases and approx. 20 wt% Fe2SiO4. The two BCC Fe phases had lattice parameters of 2.8635 and 2.8673 A. The first value is again consistent with other lattice parameters reported for Si-doped Fe, while the second value is more consistent with pure Fe. This suggests that as grains grew during annealing, some grains became Si-rich while others became Si-deficient. This result is not entirely consistent with EBSD analysis reported for these samples [14], so further analysis may be warranted.
Whole pattern fitting also indicated that the texture of the two Fe species differed. The Si-rich phase had a pronounced <001> texture, while the Si-deficient phase had a <111> texture.
One final qualitative observation can be added to this discussion. The XRPD data are not as “spotty” as would be expected for the grain sizes reported based on EBSD analysis of these specimens [14]. This qualitatively indicates that the crystallite statistics are not as poor as expected. This discrepancy can be understood by distinguishing between particle, grain, and crystallite as discussed earlier. EBSD will most often quantify grain size and the misorientation angle between neighboring grains. However, samples with high concentrations of dislocations, stacking faults, and other crystallographic defects may have a crystallite size that is smaller than the grain size measured by EBSD and other techniques. Given that the XRPD data show better-than-expected crystallite statistics and that EBSD indicates a high concentration of geometrically necessary dislocations (GNDs), it seems reasonable to conclude that the crystallite size of the Fe-3wt% Si samples was smaller than the grain size.
Parts made by additive manufacturing often have crystallite sizes that are challenging for precise and accurate X-ray powder diffraction (XRPD) measurement. The error produced in peak intensities may complicate phase analysis and may compromise quantitative phase analysis and texture analysis. The error produced in peak position will compromise lattice parameter and residual stress analysis. Collecting data with a scanning position-sensitive detector instead of a static position-sensitive detector or point detector can improve the crystallite statistics. A larger X-ray beam footprint will also improve crystallite statistics, though this may compromise spatial resolution on the specimen. Care must also be taken o preserve sufficient angular resolution of the diffraction data when using a larger X-ray beam.
Other strategies for improving XRPD analysis, not explored in this article, include using shorter wavelength X-rays (such as from a Mo anode X-ray tube) to increase the irradiated volume and the number of diffraction peaks observed in a measurement; and using parallel-beam or high-resolution optics to improve the accuracy of peak position measurements.
FeSi samples were fabricated as part of work sponsored by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Advanced Manufacturing Office, under contract DE-AC05-00OR22725.
XRPD data were collected using facilities generously provided by Prof. Prashant Kumta at the Energy Innovation Center of the University of Pittsburgh.